题目内容
 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=37
37
;f(n)=3n2-3n+1
3n2-3n+1
.分析:根据图象的规律可得相邻两项的差的规律可分析得出f(n)-f(n-1)=6(n-1),进而根据合并求和的方法求得f(n)的表达式.
解答:解:由于f(2)-f(1)=7-1=6,
f(3)-f(2)=19-7=2×6,
f(4)-f(3)=37-19=3×6,
f(5)-f(4)=61-37=4×6,…
因此,当n≥2时,有f(n)-f(n-1)=6(n-1),
所以f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+…+[f(2)-f(1)]+f(1)=6[(n-1)+(n-2)+…+2+1]+1=3n2-3n+1.
又f(1)=1=3×12-3×1+1,所以f(n)=3n2-3n+1.
当n=4时,f(4)=3×42-3×4+1=37.
故答案为:37;3n2-3n+1.
f(3)-f(2)=19-7=2×6,
f(4)-f(3)=37-19=3×6,
f(5)-f(4)=61-37=4×6,…
因此,当n≥2时,有f(n)-f(n-1)=6(n-1),
所以f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+…+[f(2)-f(1)]+f(1)=6[(n-1)+(n-2)+…+2+1]+1=3n2-3n+1.
又f(1)=1=3×12-3×1+1,所以f(n)=3n2-3n+1.
当n=4时,f(4)=3×42-3×4+1=37.
故答案为:37;3n2-3n+1.
点评:本题主要考查了数列的问题、归纳推理.属于基础题.

练习册系列答案
相关题目
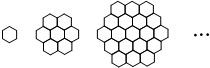 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.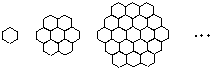 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图2为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(n)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图2为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(n)= 表示第
表示第 幅图的蜂巢总数.则
幅图的蜂巢总数.则 =___;
=___;
 表示第
表示第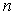 幅图的蜂巢总数.
幅图的蜂巢总数. 的值,并求
的值,并求 .
.