题目内容
已知,椭圆C以过点A(1,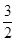 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
【答案】
(Ⅰ)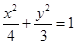 ;(Ⅱ)直线EF的斜率为定值,其值为
;(Ⅱ)直线EF的斜率为定值,其值为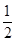 。
。
【解析】
试题分析:(1)设椭圆的右焦点,根据以右焦点为圆心,椭圆长半轴为半径的圆与直线x+ 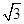 y+3=0相切,即可确定椭圆的几何量,从而可求椭圆的方程;
y+3=0相切,即可确定椭圆的几何量,从而可求椭圆的方程;
(2)设直线AE方程代入椭圆方程,利用点A(1,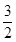 )在椭圆上,可求E的坐标,利用直线AF的斜率与AE的斜率互为相反数,可求F的坐标,从而可得直线EF的斜率,问题得解.
)在椭圆上,可求E的坐标,利用直线AF的斜率与AE的斜率互为相反数,可求F的坐标,从而可得直线EF的斜率,问题得解.
解:(Ⅰ)由题意,c=1,可设椭圆方程为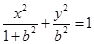 。
。
因为A在椭圆上,所以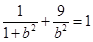 ,解得
,解得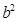 =3,
=3,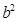 =
=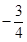 (舍去)。
(舍去)。
所以椭圆方程为 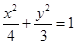 ----------------------5分
----------------------5分
(Ⅱ)设直线AE方程:得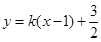 ,代入
,代入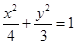 得
得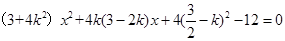
设E(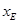 ,
,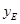 ),F(
),F(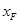 ,
,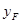 ).因为点A(1,
).因为点A(1,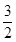 )在椭圆上,所以
)在椭圆上,所以
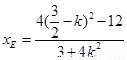 ,
,
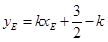 。
。
又直线AF的斜率与AE的斜率互为相反数,在上式中以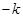 代
代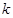 ,可得
,可得
 ,
,
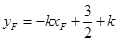 。
。
所以直线EF的斜率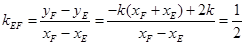 。
。
即直线EF的斜率为定值,其值为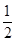 。
---------------------12分
。
---------------------12分
考点:本题主要考查了椭圆的标准方程,考查直线与椭圆的位置关系,考查直线斜率的求解,属于中档题。
点评:解题的关键是直线与椭圆方程联立,确定点的坐标,然后结合已知中斜率的关系史得到结论。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
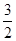 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。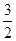 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。