题目内容
已知,椭圆C以过点A(1,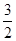 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
【答案】
(1)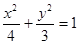
(2)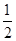
【解析】
试题分析:解:(1)由题意,c=1,可设椭圆方程为 。
。
因为A在椭圆上,所以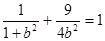 ,解得
,解得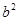 =3,
=3,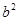 =
=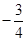 (舍去)。
(舍去)。
所以椭圆方程为 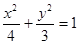 . 6分
. 6分
(2)设直线AE方程:得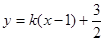 ,代入
,代入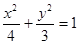 得
得
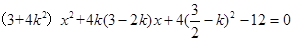
设E(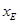 ,
,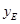 ),F(
),F(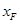 ,
,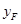 ).因为点A(1,
).因为点A(1, )在椭圆上,所以
)在椭圆上,所以
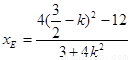 ,
,
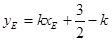 。 9分
。 9分
又直线AF的斜率与AE的斜率互为相反数,在上式中以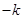 代
代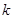 ,可得
,可得
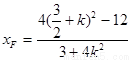 ,
,
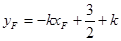 。
。
所以直线EF的斜率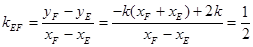 。
。
即直线EF的斜率为定值,其值为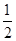 。
。
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于基础题。

练习册系列答案
相关题目
 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。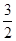 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。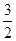 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。