题目内容
已知下列4个命题:
①若f(x)在R上为减函数,则-f(x)在R上为增函数;
②若f(x)=
,那么它的单调递增区间为[1,+∞);
③若函数f(x)=
在R上是增函数,则a的取值范围是1<a<8;
④函数f(x),g(x)在区间[-a,a](a>0)上都是奇函数,则f(x)•g(x)在区间[-a,a](a>0)是偶函数;
其中正确命题的序号是
①若f(x)在R上为减函数,则-f(x)在R上为增函数;
②若f(x)=
| x2-2x-3 |
③若函数f(x)=
|
④函数f(x),g(x)在区间[-a,a](a>0)上都是奇函数,则f(x)•g(x)在区间[-a,a](a>0)是偶函数;
其中正确命题的序号是
①④
①④
.分析:根据函数的单调性的运算法则,得①是真命题;根据函数的定义域的求法和复合函数的单调性,得②不正确;根据分段函数的单调性判别法则,得③不正确;根据函数奇偶性的定义和运算法则,可得④是真命题.由此不难得到本题答案.
解答:解:对于①,因为f(x)与-f(x)在同一单调区间上的单调性相反,
故由f(x)在R上为减函数,可得-f(x)在R上为增函数,可得①是真命题;
对于②,由于函数的定义域为{x|x2-2x-3≥0}={x|x≥3或x≤-1},
结合复合函数的单调性,得f(x)=
的单调递增区间为[3,+∞),得②不正确;
对于③,函数f(x)=
在R上是增函数,得
解之得a∈∅,故1<a<8是假命题,得③不正确;
对于④,因为f(x)、g(x)在区间[-a,a](a>0)上都是奇函数,
所以f(-x)=-f(x),g(-x)=-g(x),x∈[-a,a](a>0)
设F(x)=f(x)•g(x),得F(-x)=f(-x)g(-x)=[-f(x)][-g(x)]=f(x)•g(x),
∴F(-x)=F(x),得f(x)•g(x)在区间[-a,a](a>0)是偶函数,得④正确.
故答案为:①④
故由f(x)在R上为减函数,可得-f(x)在R上为增函数,可得①是真命题;
对于②,由于函数的定义域为{x|x2-2x-3≥0}={x|x≥3或x≤-1},
结合复合函数的单调性,得f(x)=
| x2-2x-3 |
对于③,函数f(x)=
|
|
解之得a∈∅,故1<a<8是假命题,得③不正确;
对于④,因为f(x)、g(x)在区间[-a,a](a>0)上都是奇函数,
所以f(-x)=-f(x),g(-x)=-g(x),x∈[-a,a](a>0)
设F(x)=f(x)•g(x),得F(-x)=f(-x)g(-x)=[-f(x)][-g(x)]=f(x)•g(x),
∴F(-x)=F(x),得f(x)•g(x)在区间[-a,a](a>0)是偶函数,得④正确.
故答案为:①④
点评:本题给出关于函数单调性和奇偶性的几个命题,叫我们判断它们的真假,着重考查了函数的奇偶性、单调性,及其运算法则等知识,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
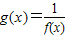 在其定义域内为减函数;
在其定义域内为减函数;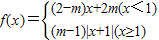 在R上是增函数,则m的取值范围是(1,2);
在R上是增函数,则m的取值范围是(1,2);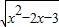 ,那么它的单调递增区间为[1,+∞);
,那么它的单调递增区间为[1,+∞);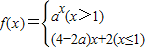 在R上是增函数,则a的取值范围是1<a<8;
在R上是增函数,则a的取值范围是1<a<8;