题目内容
已知下列4个命题:
①若f(x)为减函数,则-f(x)为增函数;
②若f(x)为增函数,则函数g(x)=
在其定义域内为减函数;
③若函数f(x)=
在R上是增函数,则a的取值范围是1<m<2;
④函数f(x),g(x)在区间[-a,a](a>0)上都是奇函数,则f(x)•g(x)在区间[-a,a](a>0)是偶函数.
其中正确命题的序号是
①若f(x)为减函数,则-f(x)为增函数;
②若f(x)为增函数,则函数g(x)=
| 1 |
| f(x) |
③若函数f(x)=
|
④函数f(x),g(x)在区间[-a,a](a>0)上都是奇函数,则f(x)•g(x)在区间[-a,a](a>0)是偶函数.
其中正确命题的序号是
①,④
①,④
.分析:①②可以运用减函数定义证明;
③是分段函数,需要保证两段都是增的,同时需要上一段的最小值大于下一段的最大值;
④运用函数奇偶性的定义证明.
③是分段函数,需要保证两段都是增的,同时需要上一段的最小值大于下一段的最大值;
④运用函数奇偶性的定义证明.
解答:解:①因为f(x)为减函数,则对其定义域内的任意x1,x2,当x1<x2时,都有f(x1)>f(x2),
令g(x)=-f(x),则g(x1)-g(x2)=-f(x1)-[-f(x2)]=f(x2)-f(x1)<0,所以-f(x1)<-f(x2),所以-f(x)为增函数,所以①正确;
②因为f(x)为增函数,则对其定义域内的任意x1,x2,当x1<x2时,都有f(x1)<f(x2),
则g(x1)-g(x2)=
-
=
,因为f(x1)<f(x2),所以f(x2)-f(x1)>0,
当f(x1)与f(x2)同号时
-
>0,g(x1)>g(x2),函数为减函数,反之,函数为增函数,所以②不正确;
③f(x)=
=
因为函数f(x)=
在R上是增函数,
所以
解得:m∈∅,所以③不正确;
④函数f(x),g(x)在区间[-a,a](a>0)上都是奇函数,则f(-x)•g(-x)=-f(x)•[-g(x)]=f(x)•g(x),
所以f(x)•g(x)在区间[-a,a](a>0)是偶函数.
所以④正确.
故答案为①④.
令g(x)=-f(x),则g(x1)-g(x2)=-f(x1)-[-f(x2)]=f(x2)-f(x1)<0,所以-f(x1)<-f(x2),所以-f(x)为增函数,所以①正确;
②因为f(x)为增函数,则对其定义域内的任意x1,x2,当x1<x2时,都有f(x1)<f(x2),
则g(x1)-g(x2)=
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| f(x2)-f(x1) |
| f(x1)f(x2) |
当f(x1)与f(x2)同号时
| 1 |
| f(x1) |
| 1 |
| f(x2) |
③f(x)=
|
=
|
因为函数f(x)=
|
所以
|
④函数f(x),g(x)在区间[-a,a](a>0)上都是奇函数,则f(-x)•g(-x)=-f(x)•[-g(x)]=f(x)•g(x),
所以f(x)•g(x)在区间[-a,a](a>0)是偶函数.
所以④正确.
故答案为①④.
点评:本题考查了命题真假的判断,考查了判断函数单调性和奇偶性的方法,结论是:函数f(x)与-f(x)在相同区间上单调性相反,在相同定义域内,两个奇函数的乘积为偶函数.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
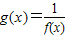 在其定义域内为减函数;
在其定义域内为减函数;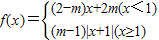 在R上是增函数,则m的取值范围是(1,2);
在R上是增函数,则m的取值范围是(1,2);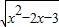 ,那么它的单调递增区间为[1,+∞);
,那么它的单调递增区间为[1,+∞);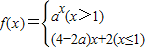 在R上是增函数,则a的取值范围是1<a<8;
在R上是增函数,则a的取值范围是1<a<8;