题目内容
已知函数 .
.(1)若函数f(x)在[1,+∞)上为增函数,求正实数a的取值范围;
(2)当a=1时,求f(x)在
 上的最大值和最小值;
上的最大值和最小值;(3)当a=1时,求证:对大于1的任意正整数n,都有
 .
.
【答案】分析:(1)对函数f(x)进行求导,令导函数大于等于0在[1,+∞)上恒成立即可求出a的范围.
(2)将a=1代入函数f(x)的解析式,判断其单调性进而得到最大值和最小值.
(3)先判断函数f(x)的单调性,令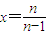 代入函数f(x)根据单调性得到不等式
代入函数f(x)根据单调性得到不等式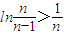 ,令n=1,2,…代入可证.
,令n=1,2,…代入可证.
解答:解:(1)∵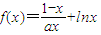
∴
∵函数f(x)在[1,+∞)上为增函数
∴ 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,
∴ax-1≥0对x∈[1,+∞)恒成立,即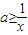 对x∈[1,+∞)恒成立
对x∈[1,+∞)恒成立
∴a≥1
(2)当a=1时,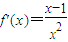 ,
,
∴当 时,f′(x)<0,故f(x)在
时,f′(x)<0,故f(x)在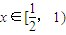 上单调递减;
上单调递减;
当x∈(1,2]时,f′(x)>0,故f(x)在x∈(1,2]上单调递增,
∴f(x)在区间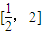 上有唯一极小值点,故f(x)min=f(x)极小值=f(1)=0
上有唯一极小值点,故f(x)min=f(x)极小值=f(1)=0
又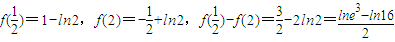
∵e3>16
∴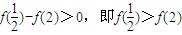
∴f(x)在区间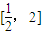 上的最大值
上的最大值
综上可知,函数f(x)在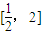 上的最大值是1-ln2,最小值是0.
上的最大值是1-ln2,最小值是0.
(3)当a=1时, ,
,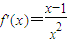 ,
,
故f(x)在[1,+∞)上为增函数.
当n>1时,令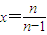 ,则x>1,故f(x)>f(1)=0
,则x>1,故f(x)>f(1)=0
∴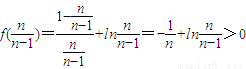 ,即
,即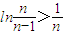
∴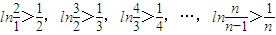
∴
∴
即对大于1的任意正整数n,都有
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.
(2)将a=1代入函数f(x)的解析式,判断其单调性进而得到最大值和最小值.
(3)先判断函数f(x)的单调性,令
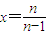 代入函数f(x)根据单调性得到不等式
代入函数f(x)根据单调性得到不等式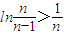 ,令n=1,2,…代入可证.
,令n=1,2,…代入可证.解答:解:(1)∵
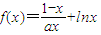
∴

∵函数f(x)在[1,+∞)上为增函数
∴
 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,∴ax-1≥0对x∈[1,+∞)恒成立,即
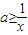 对x∈[1,+∞)恒成立
对x∈[1,+∞)恒成立∴a≥1
(2)当a=1时,
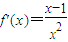 ,
,∴当
 时,f′(x)<0,故f(x)在
时,f′(x)<0,故f(x)在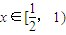 上单调递减;
上单调递减;当x∈(1,2]时,f′(x)>0,故f(x)在x∈(1,2]上单调递增,
∴f(x)在区间
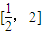 上有唯一极小值点,故f(x)min=f(x)极小值=f(1)=0
上有唯一极小值点,故f(x)min=f(x)极小值=f(1)=0又
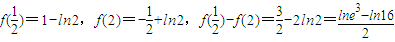
∵e3>16
∴
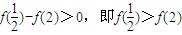
∴f(x)在区间
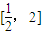 上的最大值
上的最大值
综上可知,函数f(x)在
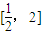 上的最大值是1-ln2,最小值是0.
上的最大值是1-ln2,最小值是0.(3)当a=1时,
 ,
,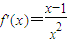 ,
,故f(x)在[1,+∞)上为增函数.
当n>1时,令
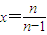 ,则x>1,故f(x)>f(1)=0
,则x>1,故f(x)>f(1)=0∴
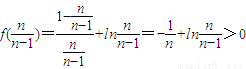 ,即
,即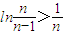
∴
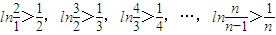
∴

∴

即对大于1的任意正整数n,都有

点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目





 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。