题目内容
(本题满分12分)已知数列![]() 的前
的前![]() 项之积与第
项之积与第![]() 项的和等于1
项的和等于1![]() . (1)求证
. (1)求证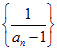 是等差数列,并求
是等差数列,并求![]() 的通项公式;(2)设
的通项公式;(2)设![]() ,求证
,求证![]() .
.
(1)![]()
解析:
(1)![]() ,易知
,易知![]()
则![]() …① ,
…① ,![]() …②
…②
两式相除得![]() ,即
,即![]() ,∴
,∴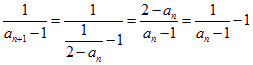 .
.
∴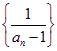 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,在已知中令
为公差的等差数列,在已知中令![]() 可得
可得![]()
∴![]() ,∴
,∴![]() …6分
…6分
(2)由![]() (
(![]() )
)
所以![]() (
(![]() )
)
又因为![]()
![]()
![]() ,
,![]()
∴![]()
![]()
![]()
综上 ![]() 成立. …12分
成立. …12分

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
题目内容
(本题满分12分)已知数列![]() 的前
的前![]() 项之积与第
项之积与第![]() 项的和等于1
项的和等于1![]() . (1)求证
. (1)求证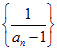 是等差数列,并求
是等差数列,并求![]() 的通项公式;(2)设
的通项公式;(2)设![]() ,求证
,求证![]() .
.
(1)![]()
(1)![]() ,易知
,易知![]()
则![]() …① ,
…① ,![]() …②
…②
两式相除得![]() ,即
,即![]() ,∴
,∴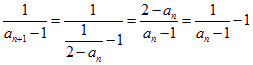 .
.
∴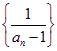 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,在已知中令
为公差的等差数列,在已知中令![]() 可得
可得![]()
∴![]() ,∴
,∴![]() …6分
…6分
(2)由![]() (
(![]() )
)
所以![]() (
(![]() )
)
又因为![]()
![]()
![]() ,
,![]()
∴![]()
![]()
![]()
综上 ![]() 成立. …12分
成立. …12分

 每课必练系列答案
每课必练系列答案