题目内容
【题目】选修4-5:不等式选讲
已知函数![]() (
(![]() ).
).
(1)若![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)若对于任意的![]() ,
,![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】见解析
【解析】(1) 当![]() 时,
时,![]() .
.
若x≤1,则![]() ,于是由
,于是由![]() 解得x<
解得x<![]() .综合得x<
.综合得x<![]() .
.
若1<x<2,则![]() ,显然
,显然![]() 不成立 .
不成立 .
若x≥2,则![]() ,于是由
,于是由![]() 解得x>
解得x>![]() .综合得x>
.综合得x>![]() .
.
∴ 不等式![]() 的解集为{x| x<
的解集为{x| x<![]() ,或x>
,或x>![]() }. …………………………5分
}. …………………………5分
(2)![]() 等价于
等价于![]() .令g(x)= f(x)-x.
.令g(x)= f(x)-x.
当-1≤x≤1时,g(x)=1+a-3x,显然g(x)min=g(1)=a-2.
当1<x<a时,g(x)=a-1-x,此时-1=g(a)<g(x)<g(1)=a-2.
当a≤x≤3时,g(x)=x-a-1,g(x)min=g(a)= -1≤g(1)=a-2.
∴ 当x∈[1,3]时,g(x)min= -1.
∴![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() . ……………………………………………10分
. ……………………………………………10分
【命题意图】本题考查含绝对值不等式的解法,不等式恒成立等基础知识,意在考查分类讨论的数学思想方法,以及学生的分析问题、解决问题的能力.

【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)计算回归系数 ![]() ,
, ![]() .公式为
.公式为 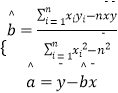 .
.
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(2)若![]() 队平均身高为
队平均身高为![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测![]() 队的平均得分.(精确到个位)
队的平均得分.(精确到个位)
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为
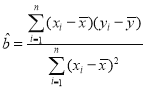 ,
,![]() .
.
