题目内容
10.已知等差数列{an}的前n项和为Sn,且满足a3=2,S5=a7.(Ⅰ)求数列{an}的通项公式an及Sn;
(Ⅱ)若a4,a4+m,a4+n(m,n∈N*)成等比数列,求n的最小值.
分析 (Ⅰ)设公差为d,利用a3=2,S5=a7,建立方程组,求出a1=-2,d=2,即可求数列{an}的通项公式an及Sn;
(Ⅱ)若a4,a4+m,a4+n(m,n∈N*)成等比数列,可得$n=\frac{1}{2}{(m+2)^2}-2$,考察函数$f(x)=\frac{1}{2}{(x+2)^2}-2$,知f(x)在(0,+∞)上单调递增,即可求n的最小值.
解答 解:(Ⅰ)设公差为d,
由题意,得$\left\{\begin{array}{l}{a_1}+2d=2\\ 5{a_1}+\frac{1}{2}×5×4d={a_1}+6d\end{array}\right.$…(4分)
解得a1=-2,d=2,…(5分)
所以an=-2+(n-1)×2=2n-4,…(6分)
${S_n}=-2n+\frac{1}{2}n(n-1)×2={n^2}-3n$. …(7分)
(Ⅱ)因为a4,a4+m,a4+n成等比数列,
所以$a_{4+m}^2={a_4}{a_{4+n}}$,…(9分)
即(2m+4)2=4(2n+4),…(10分)
化简,得$n=\frac{1}{2}{(m+2)^2}-2$,…(11分)
考察函数$f(x)=\frac{1}{2}{(x+2)^2}-2$,知f(x)在(0,+∞)上单调递增,
又因为$f(1)=\frac{5}{2}$,f(2)=6,n∈N*,
所以当m=2时,n有最小值6. …(13分)
点评 本题考查等差数列的通项与求和,考查等比数列的性质,确定数列的通项是关键.

练习册系列答案
相关题目
18.复数z=(3-2i)i,则z-2$\overline{z}$=( )
| A. | -2-9i | B. | -2+9i | C. | 2-9i | D. | 2+9i |
5.复数z满足z•i=3-i,则在复平面内,复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.设m∈R,过定点A的动直线mx+y-1=0与过定点B的动直线x-my+m+2=0交于点P(x,y),则|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|的
最大值为( )
最大值为( )
| A. | 2 | B. | $\sqrt{2}$+1 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+2 |
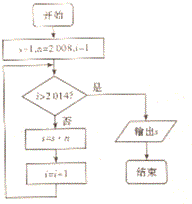 如图所示的流程图,根据最后输出的变量s的值,得s的末位数值是4.
如图所示的流程图,根据最后输出的变量s的值,得s的末位数值是4. 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.