题目内容
设i是虚数单位,集合M={1,i},N={-
,
},则M∪N为( )
| 1 |
| i |
| 1-i |
| 1+i |
分析:先将N化简,再求M∪N.
解答:解:由于
=i,
=
=
=-i,所以N={i.-i},
M∪N={1,i,-i}
故选C.
| 1 |
| -i |
| 1-i |
| 1+i |
| (1-i)2 |
| (1+i)(1-i) |
| -2i |
| 2 |
M∪N={1,i,-i}
故选C.
点评:本题考查了复数代数形式的混合运算,集合的基本运算.属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
设i是虚数单位,集合A={1,i},B={-
,
},则A∪B为( )
| 1 |
| i |
| (1-i)2 |
| 2 |
| A、A | B、B |
| C、{1,i,-i} | D、{-1,1,i} |
设i是虚数单位,在复平面上,满足|z+1+i|+|z-1-i|=2
的复数z对应的点Z的集合是( )
| 2 |
| A、圆 | B、椭圆 | C、双曲线 | D、线段 |
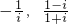 ,则M∪N为
,则M∪N为 ,则M∪N为( )
,则M∪N为( )