题目内容
已知sinx+sinα=
，求关于x的函数y=1+sinx+sin2α的最值．
【答案】分析：有偶题意求出sinα，并由正弦函数的值域求出sinx的范围，代入解析式并且配方，再由sinx的范围和二次函数的单调性求出函数的最值．
解答：解：由sinx+sinα=
得，sinα=
-sinx，
则-1≤
-sinx≤1，解得
，即
，
代入解析式得，
=
=
，
∵
，
∴当sinx=1时，函数取到最大值是y=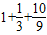
=
，
当sinx=
时，函数取到最小值是y=
．
点评：本题考查了整体思想，配方法，以及正弦函数的值域应用，以及二次函数的性质应用，属于综合题．
解答：解：由sinx+sinα=
得，sinα=-sinx，则-1≤
-sinx≤1，解得，即，代入解析式得，
==，∵
，∴当sinx=1时，函数取到最大值是y=
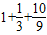=，当sinx=
时，函数取到最小值是y=．点评：本题考查了整体思想，配方法，以及正弦函数的值域应用，以及二次函数的性质应用，属于综合题．
练习册系列答案
相关题目