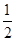题目内容
已知P是△ABC内一点,且满足 =0,记△ABP、△BCP、△ACP的面积依次为S1、S2、S3,则S1:S2:S3 ________.
=0,记△ABP、△BCP、△ACP的面积依次为S1、S2、S3,则S1:S2:S3 ________.
3:1:2
分析:有已知的等式变形可得∴ =-6
=-6 ,
,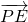 =-
=-
 ,P到BC的距离等于A到BC的距离的
,P到BC的距离等于A到BC的距离的 ,P到AC的距离等于B到AC的距离的
,P到AC的距离等于B到AC的距离的 .从而,S2 =
.从而,S2 = S,S3 =
S,S3 = S,S1 =S-S2-S3 =
S,S1 =S-S2-S3 = S.
S.
解答: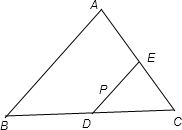 解:如图:设D、E 分别为BC、AC的中点,
解:如图:设D、E 分别为BC、AC的中点,
∵ =0,∴
=0,∴ -
- =-3(
=-3( +
+ ),
),
∴ =-3×2
=-3×2 =-6
=-6 ,
,
同理由( +
+ )=-2(
)=-2( +
+ ),即 2
),即 2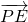 =-2×
=-2× ,
,
∴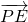 =-
=-
 .∴P到BC的距离等于A到BC的距离的
.∴P到BC的距离等于A到BC的距离的 ,
,
设△ABC的面积为S,则S2 = S.
S.
P到AC的距离等于B到AC的距离的 ,
,
∴S3 = S.∴S1 =S-S2-S3 =
S.∴S1 =S-S2-S3 = S.
S.
∴S1:S2:S3= S:
S: S=
S= S=3:1:2,
S=3:1:2,
故答案为:3:1:2.
点评:本题考查共线向量的意义,两个同底的三角形的面积之比等于底上的高之比,体现了数形结合的数学思想.
分析:有已知的等式变形可得∴
 =-6
=-6 ,
,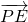 =-
=-
 ,P到BC的距离等于A到BC的距离的
,P到BC的距离等于A到BC的距离的 ,P到AC的距离等于B到AC的距离的
,P到AC的距离等于B到AC的距离的 .从而,S2 =
.从而,S2 = S,S3 =
S,S3 = S,S1 =S-S2-S3 =
S,S1 =S-S2-S3 = S.
S.解答:
 解:如图:设D、E 分别为BC、AC的中点,
解:如图:设D、E 分别为BC、AC的中点,∵
 =0,∴
=0,∴ -
- =-3(
=-3( +
+ ),
),∴
 =-3×2
=-3×2 =-6
=-6 ,
,同理由(
 +
+ )=-2(
)=-2( +
+ ),即 2
),即 2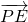 =-2×
=-2× ,
,∴
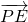 =-
=-
 .∴P到BC的距离等于A到BC的距离的
.∴P到BC的距离等于A到BC的距离的 ,
,设△ABC的面积为S,则S2 =
 S.
S.P到AC的距离等于B到AC的距离的
 ,
,∴S3 =
 S.∴S1 =S-S2-S3 =
S.∴S1 =S-S2-S3 = S.
S.∴S1:S2:S3=
 S:
S: S=
S= S=3:1:2,
S=3:1:2,故答案为:3:1:2.
点评:本题考查共线向量的意义,两个同底的三角形的面积之比等于底上的高之比,体现了数形结合的数学思想.

练习册系列答案
相关题目
已知P是△ABC所在平面内一点,
+
+2
=
,现将一粒黄豆随机撒在△ABC内,则黄豆落在△APC内的概率是( )
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
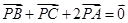 ,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )
,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )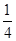 B.
B.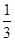 C.
C.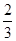 D.
D.