题目内容
设P(x,y)为曲线y=|| 1 | 2 |
分析:首先画出曲线y=|
x2-1|的图象.根据图象分-
<x<
,x<-
,或x>
两种情况讨论|PA|的最小值.再通过a的取值.a>4时,a2-4a>0,即a-1>
,此时|PA|min=
;当1<a≤4时,a2-4a≤0,即a-1≤
,此时|PA|min=a-1.从而确定|PA|的最小值.
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2a+1 |
| 2a+1 |
| 2a+1 |
解答:解: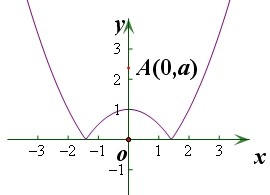 令
令
x2-1=0,则
x=±
.
∵a>1
∴如图可知,
当-
<x<
时,|PA|≥a-1,
当x<-
,或x>
时,
|PA|=
=
=
=
≥
.
∵(a-1)2-(2a+1)=a2-4a,
∴a>4时,a2-4a>0,即a-1>
,
此时|PA|min=
;
当1<a≤4时,a2-4a≤0,即a-1≤
,
此时|PA|min=a-1.
 令
令| 1 |
| 2 |
x=±
| 2 |
∵a>1
∴如图可知,
当-
| 2 |
| 2 |
当x<-
| 2 |
| 2 |
|PA|=
| x2+(y-a)2 |
=
x2+(
|
=
|
=
(
|
| 2a+1 |
∵(a-1)2-(2a+1)=a2-4a,
∴a>4时,a2-4a>0,即a-1>
| 2a+1 |
此时|PA|min=
| 2a+1 |
当1<a≤4时,a2-4a≤0,即a-1≤
| 2a+1 |
此时|PA|min=a-1.
点评:本题考查数形结合以及分类讨论的思想,两点间的距离公式,不等式的解法及应用等知识的综合运用.属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的点的轨迹.
的点的轨迹. 的取值范围.
的取值范围.