题目内容
(选做题)设P(x,y) 是曲线C:
(θ为参数)上任意一点,则
的取值范围是
|
| y |
| x |
[-
,
]
| ||
| 3 |
| ||
| 3 |
[-
,
]
.
| ||
| 3 |
| ||
| 3 |
分析:求出圆的普通方程,利用
的几何意义,圆上的点与坐标原点连线的斜率,求出斜率的范围即可.
| y |
| x |
解答:解:曲线C的方程可化为(x+2)2+y2=1,(3分)
可见曲线C是以点C(-2,0)为圆心半径为1的圆(4分)
设点P(x,y)为曲线C上一动点,
则
=kOP,即O、P两点连线的斜率(6分)
当P的坐标为(-
,
)时,
有最小值为-
,
当P的坐标为(-
,-
)时,
有最大值为
,
所以
的取值范围是[-
,
].
故答案为:[-
,
].
可见曲线C是以点C(-2,0)为圆心半径为1的圆(4分)
设点P(x,y)为曲线C上一动点,
则
| y |
| x |
当P的坐标为(-
| 3 |
| 2 |
| ||
| 2 |
| y |
| x |
| ||
| 3 |
当P的坐标为(-
| 3 |
| 2 |
| ||
| 2 |
| y |
| x |
| ||
| 3 |
所以
| y |
| x |
| ||
| 3 |
| ||
| 3 |
故答案为:[-
| ||
| 3 |
| ||
| 3 |
点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
相关题目
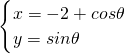 (θ为参数)上任意一点,则
(θ为参数)上任意一点,则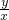 的取值范围是________.
的取值范围是________. (θ为参数)上任意一点,则
(θ为参数)上任意一点,则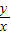 的取值范围是 .
的取值范围是 . (θ为参数)上任意一点,则
(θ为参数)上任意一点,则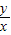 的取值范围是 .
的取值范围是 .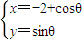 (θ为参数)上任意一点,则
(θ为参数)上任意一点,则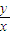 的取值范围是 .
的取值范围是 .