题目内容
(本小题满分16分)
已知函数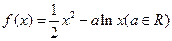
(1)若函数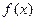 在
在 处的切线方程为
处的切线方程为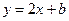 ,求
,求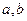 的值;
的值;
(2)任取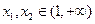 ,且
,且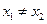 ,恒有
,恒有 ,求
,求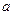 的取值范围;
的取值范围;
(3)讨论方程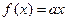 的解的个数,并说明理由。
的解的个数,并说明理由。
已知函数
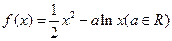
(1)若函数
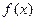 在
在 处的切线方程为
处的切线方程为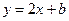 ,求
,求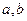 的值;
的值;(2)任取
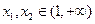 ,且
,且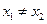 ,恒有
,恒有 ,求
,求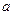 的取值范围;
的取值范围;(3)讨论方程
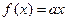 的解的个数,并说明理由。
的解的个数,并说明理由。(1)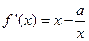
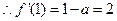 ,解得
,解得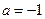 ,切点为
,切点为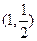 代入直线方程解得
代入直线方程解得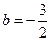 …………………………4分
…………………………4分
(2)不妨假设 ,则
,则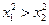 ,所以
,所以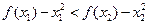 (*)
(*)
令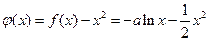
则(*)等价于函数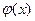 在区间
在区间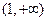 上为单调减函数
上为单调减函数
即等价于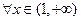 ,不等式
,不等式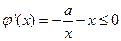 恒成立
恒成立
解得: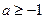 …………………………………………………………………………………………………9分
…………………………………………………………………………………………………9分
(3)令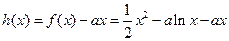 (
(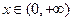
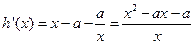
①当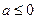 时,在
时,在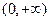 上,
上, ,函数
,函数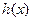 在
在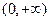 上为增函数且当
上为增函数且当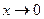 时,
时,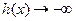 ,当
,当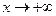 时,
时,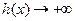
由此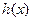 的图象与
的图象与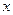 轴有且仅有一个公共点,即方程
轴有且仅有一个公共点,即方程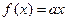 有且仅有一个实根。
有且仅有一个实根。
②当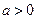 时,方程
时,方程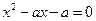 有两个不相等的实数根,并且一个正根一个负根,不妨设正根为
有两个不相等的实数根,并且一个正根一个负根,不妨设正根为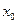
则当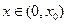 时,
时,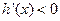 ,
,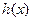 为单调递减函数;当
为单调递减函数;当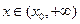 时,
时, ,
,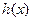 为单调递增函数,故函数
为单调递增函数,故函数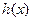 有最小值
有最小值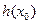
(ⅰ)当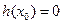 时,
时,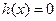 有且只有一个实数根,即方程
有且只有一个实数根,即方程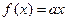 有且仅有一个实根。
有且仅有一个实根。
此时有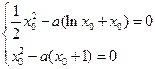 ,变形得
,变形得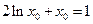 (**)
(**)
构造函数 在
在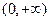 上为单调增函数,方程(**)等价于
上为单调增函数,方程(**)等价于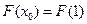
解得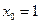 ,代入原方程组,解得
,代入原方程组,解得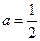
(ⅱ)当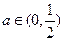 时,
时,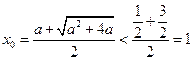 ,
,
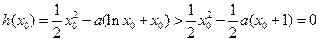
所以方程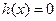 无实数根,即方程
无实数根,即方程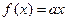 没有实数根
没有实数根
(ⅰⅱ)当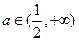 时,类似可以求得
时,类似可以求得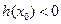
所以方程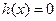 有两个实数根,即方程
有两个实数根,即方程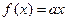 有两个实数根
有两个实数根
综上,当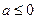 或
或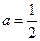 时,方程
时,方程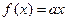 有且仅有一个实根
有且仅有一个实根
当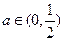 时,方程
时,方程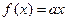 没有实数根
没有实数根
当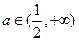 时,方程
时,方程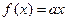 有两个实数根………………………………………………16分
有两个实数根………………………………………………16分
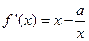
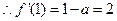 ,解得
,解得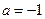 ,切点为
,切点为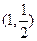 代入直线方程解得
代入直线方程解得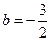 …………………………4分
…………………………4分(2)不妨假设
 ,则
,则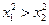 ,所以
,所以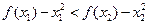 (*)
(*)令
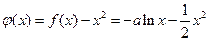
则(*)等价于函数
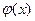 在区间
在区间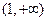 上为单调减函数
上为单调减函数即等价于
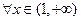 ,不等式
,不等式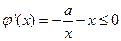 恒成立
恒成立解得:
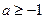 …………………………………………………………………………………………………9分
…………………………………………………………………………………………………9分(3)令
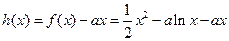 (
(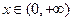
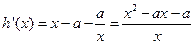
①当
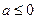 时,在
时,在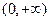 上,
上, ,函数
,函数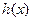 在
在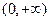 上为增函数且当
上为增函数且当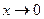 时,
时,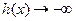 ,当
,当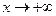 时,
时,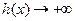
由此
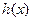 的图象与
的图象与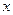 轴有且仅有一个公共点,即方程
轴有且仅有一个公共点,即方程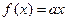 有且仅有一个实根。
有且仅有一个实根。②当
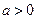 时,方程
时,方程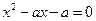 有两个不相等的实数根,并且一个正根一个负根,不妨设正根为
有两个不相等的实数根,并且一个正根一个负根,不妨设正根为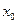
则当
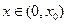 时,
时,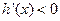 ,
,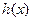 为单调递减函数;当
为单调递减函数;当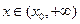 时,
时, ,
,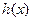 为单调递增函数,故函数
为单调递增函数,故函数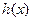 有最小值
有最小值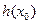
(ⅰ)当
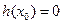 时,
时,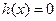 有且只有一个实数根,即方程
有且只有一个实数根,即方程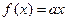 有且仅有一个实根。
有且仅有一个实根。此时有
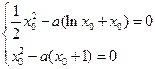 ,变形得
,变形得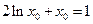 (**)
(**)构造函数
 在
在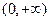 上为单调增函数,方程(**)等价于
上为单调增函数,方程(**)等价于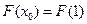
解得
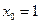 ,代入原方程组,解得
,代入原方程组,解得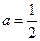
(ⅱ)当
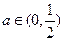 时,
时,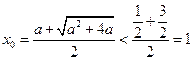 ,
,
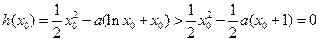
所以方程
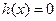 无实数根,即方程
无实数根,即方程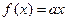 没有实数根
没有实数根(ⅰⅱ)当
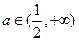 时,类似可以求得
时,类似可以求得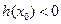
所以方程
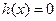 有两个实数根,即方程
有两个实数根,即方程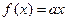 有两个实数根
有两个实数根综上,当
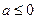 或
或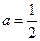 时,方程
时,方程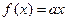 有且仅有一个实根
有且仅有一个实根当
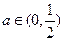 时,方程
时,方程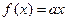 没有实数根
没有实数根当
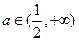 时,方程
时,方程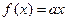 有两个实数根………………………………………………16分
有两个实数根………………………………………………16分略

练习册系列答案
相关题目
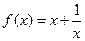
 的奇偶性.
的奇偶性.
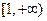 内单调性并用定义证明;
内单调性并用定义证明; 上的最小值.
上的最小值.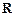 上的函数
上的函数 若关于
若关于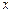 的方程
的方程 有3个不同的实数解
有3个不同的实数解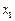 ,
,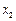 ,
, ,则
,则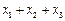 等于 ( )
等于 ( )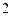
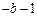

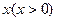 户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高
户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高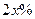 ,而从事水产加工的农民平均每户的年收入将为
,而从事水产加工的农民平均每户的年收入将为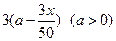 万元.
万元.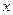 户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求
户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求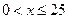 ,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求
,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求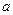 的最大值.
的最大值. 若
若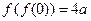 ,则实数
,则实数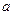 = .
= .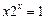 根的个数为 ▲
根的个数为 ▲ 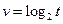
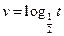
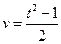
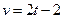
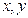 ,定义运算
,定义运算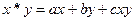 ,其中
,其中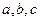 为常数,等号右边的运算是通常意义的加、乘运算.现已知
为常数,等号右边的运算是通常意义的加、乘运算.现已知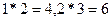 ,且有一个非零实数
,且有一个非零实数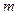 ,使得对任意实数
,使得对任意实数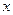 ,都有
,都有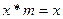 ,则
,则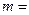 ( )
( )