题目内容
函数 的定义域为
的定义域为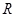 ,
,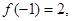 对任意
对任意
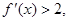 则
则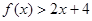
的解集为
A.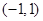 | B.(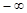 ,+ ,+ ) ) |
C.(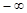 , ,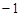 ) ) | D.(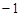 ,+ ,+ ) ) |
D
解析试题分析:设F(x)=f(x)-(2x+4),
则F(-1)=f(-1)-(-2+4)=2-2=0,
又对任意x∈R,f′(x)>2,所以F′(x)=f′(x)-2>0,
即F(x)在R上单调递增,
则F(x)>0的解集为(-1,+∞),
即f(x)>2x+4的解集为(-1,+∞).故选D
考点:用函数思想求不等式的解集

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
函数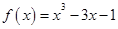 ,若对于区间[-3,2]上的任意x1,x2,都有 | f(x1)-f (x2)|≤ t,则实数t的最小值是( )
,若对于区间[-3,2]上的任意x1,x2,都有 | f(x1)-f (x2)|≤ t,则实数t的最小值是( )
| A.20 | B.18 | C.3 | D.0 |
下列求导数运算正确的是( )
A.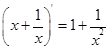 | B.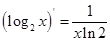 |
C.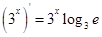 | D.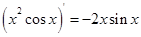 |
设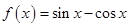 ,则
,则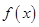 在
在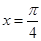 处的导数
处的导数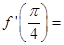 ( )
( )
A.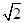 | B.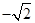 | C.0 | D. |
若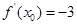 ,则
,则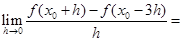 ( )
( )
A.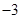 | B.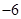 | C.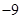 | D.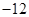 |
设 是定义在R上的奇函数,且
是定义在R上的奇函数,且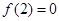 ,当x>0时,有
,当x>0时,有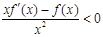 恒成立,则不等式
恒成立,则不等式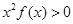 的解集是 ( )
的解集是 ( )
| A.(2,0) ∪(2,+∞) | B.(2,0) ∪(0,2) |
| C.(∞,2)∪(2,+∞) | D.(∞,2)∪(0,2) |
已知函数f(x)=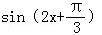 ,要得到
,要得到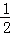 f′(x)的图象,只需将f(x)的图象( )个单位.
f′(x)的图象,只需将f(x)的图象( )个单位.
A.向右平移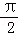 | B.向左平移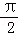 |
C.向右平移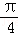 | D.向左平移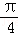 |
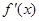 是函数
是函数 的导函数,将
的导函数,将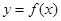 和
和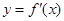 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )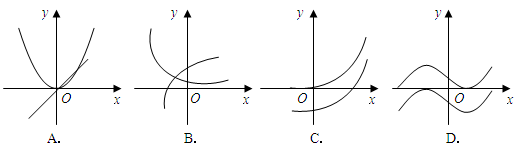
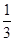 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )