题目内容
设数列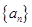 的前
的前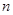 项和为
项和为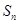 .已知
.已知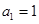 ,
,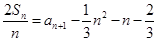 ,
,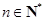 .
.
(Ⅰ) 求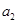 的值;
的值;
(Ⅱ) 求数列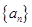 的通项公式;
的通项公式;
(Ⅲ) 证明:对一切正整数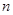 ,有
,有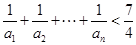 .
.
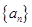 的前
的前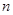 项和为
项和为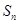 .已知
.已知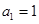 ,
,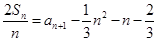 ,
,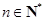 .
.(Ⅰ) 求
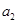 的值;
的值;(Ⅱ) 求数列
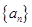 的通项公式;
的通项公式;(Ⅲ) 证明:对一切正整数
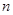 ,有
,有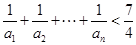 .
.(Ⅰ) 4(Ⅱ) 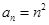 (Ⅲ)见解析
(Ⅲ)见解析
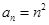 (Ⅲ)见解析
(Ⅲ)见解析(Ⅰ) 依题意,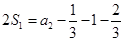 ,又
,又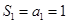 ,所以
,所以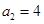 ;
;
(Ⅱ) 当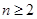 时,
时, ,
,
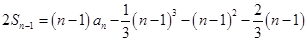
两式相减得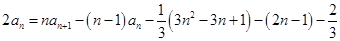
整理得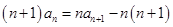 ,即
,即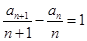 ,又
,又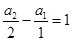
故数列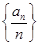 是首项为
是首项为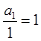 ,公差为
,公差为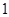 的等差数列,
的等差数列,
所以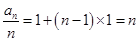 ,所以
,所以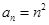 .
.
(Ⅲ) 当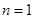 时,
时,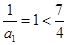 ;当
;当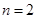 时,
时,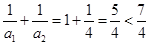 ;
;
当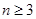 时,
时,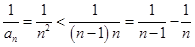 ,此时
,此时
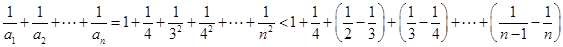
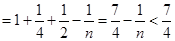
综上,对一切正整数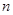 ,有
,有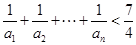 .
.
(1)直接将n换为2代入递推式求解;(2)借助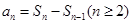 进行递推转化,进而构造数列
进行递推转化,进而构造数列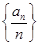 为等差数列是解题的关键,考查了学生对式子的操作能力和转化能力.(3)借助放缩法进行证明,放缩的关键是
为等差数列是解题的关键,考查了学生对式子的操作能力和转化能力.(3)借助放缩法进行证明,放缩的关键是 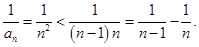
【考点定位】本题考查数列的通项公式和数列求和问题,以及不等式的证明.
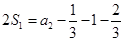 ,又
,又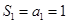 ,所以
,所以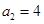 ;
;(Ⅱ) 当
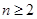 时,
时, ,
,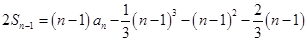
两式相减得
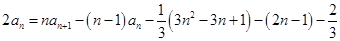
整理得
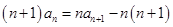 ,即
,即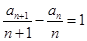 ,又
,又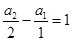
故数列
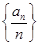 是首项为
是首项为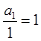 ,公差为
,公差为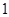 的等差数列,
的等差数列,所以
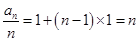 ,所以
,所以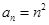 .
.(Ⅲ) 当
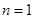 时,
时,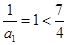 ;当
;当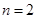 时,
时,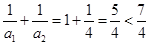 ;
;当
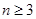 时,
时,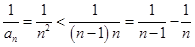 ,此时
,此时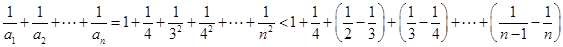
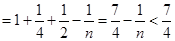
综上,对一切正整数
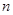 ,有
,有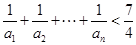 .
.(1)直接将n换为2代入递推式求解;(2)借助
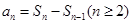 进行递推转化,进而构造数列
进行递推转化,进而构造数列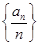 为等差数列是解题的关键,考查了学生对式子的操作能力和转化能力.(3)借助放缩法进行证明,放缩的关键是
为等差数列是解题的关键,考查了学生对式子的操作能力和转化能力.(3)借助放缩法进行证明,放缩的关键是 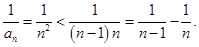
【考点定位】本题考查数列的通项公式和数列求和问题,以及不等式的证明.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
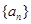 满足
满足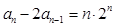
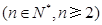 ,且
,且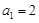 .
.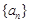 的通项公式;
的通项公式; 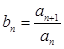 ,当数列
,当数列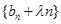 为递增数列时,求正实数
为递增数列时,求正实数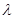 的取值范围.
的取值范围.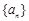 的前n项和为
的前n项和为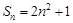 ,则an=( )
,则an=( )

 ,
, ,
, 成等比数列.
成等比数列.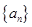 的通项公式;
的通项公式;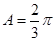 =1,d=3确定的等差数列
=1,d=3确定的等差数列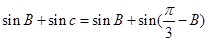 ,当
,当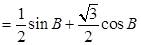 =298是,n等于
=298是,n等于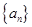 是首项
是首项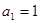 的等比数列,其前
的等比数列,其前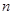 项和
项和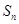 中,
中,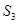 、
、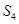 、
、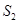 成等差数列.
成等差数列.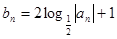 ,求数列{
,求数列{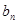 }的前
}的前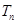 ;
;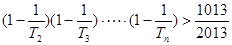 的最大正整数
的最大正整数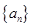 的前
的前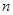 项和是
项和是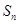 ,若
,若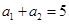 ,
,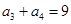 ,则
,则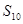 的值为
的值为 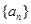 为等差数列,且a3=5,a5=9;数列
为等差数列,且a3=5,a5=9;数列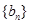 的前n项和为Sn,且Sn+bn="2."
的前n项和为Sn,且Sn+bn="2." 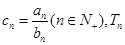 为数列
为数列 的前n项和,求
的前n项和,求 .
. 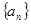 和
和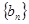 的前
的前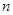 项和分别是
项和分别是 ,
, ,已知
,已知 ,则
,则


