题目内容
求与y轴相切,且与圆C:x2+y2-10x=0:(1)内切的动圆圆心的轨迹方程;(2)外切的动圆圆心的轨迹方程.
答案:
解析:
提示:
解析:
|
解:设动圆圆心坐标为P(x,y),由于它与y轴相切,故设动圆P的半径r=|x|. (1)已知圆C的圆心为C(5,0),半径r1=5,由两圆内切,结合图形可知:r=x>0. 则|CP|=|5-r|=|5-x|.∴|CP|2=(5-x)2. 则(x-5)2+y2=(5-x)2,化简得y=0(x>0),即为所求动圆圆心的轨迹方程. (2)圆C的圆心为C(5,0),半径r1=5,由两圆外切,可分两种情况讨论: ①当x>0时,则|CP|=r+5=x+5.∴|CP|2=(x+5)2. 则(x-5)2+y2=(x+5)2,∴y2=20x(x>0). ②当x<0时,则r=|x|=-x,|CP|=r+5=5-x,|CP|2=(5-x)2. 则(x-5)2+y2=(5-x)2,∴y=0(x<0). 故两个圆外切时,圆心P的轨迹方程为 |
提示:
|
考查轨迹方程的求法.先设出动圆圆心的坐标,再根据相切的几何关系寻找规律. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
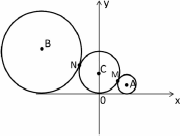
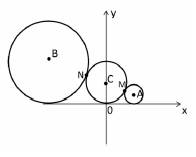
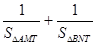 的最小值为2,求直线AB的方程.
的最小值为2,求直线AB的方程.