题目内容
设双曲线
的右焦点为F，右准线l与两条渐近线交于P，Q两点，如果△PQF是直角三角形，则双曲线的离心率为（ ）A．2
B．
C．
D．
【答案】分析：本题中由双曲线的对称性可得|PM|=|MQ|，又由△PQF是直角三角形得到|MF|=|MP|，通过这个等量关系可以得到a=b，即 
=1，代入求离心率的公式，得到e=
．
解答：解：依题意可知右准线方程l：x=
，渐近线方程y=±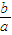
x，则有P（ 
，
），F（c，0）
由题意|MF|=|MP|，即|c-
|=
整理得 
因为c2-a2=b2，将其代入上式得a=b
所以e=
=
=
故选C．
点评：本题主要考查了双曲线的简单性质．解题的关键是熟练掌握双曲线中渐近线、准线、焦距等基本知识．
=1，代入求离心率的公式，得到e=．解答：解：依题意可知右准线方程l：x=
，渐近线方程y=±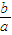x，则有P（ ，），F（c，0）由题意|MF|=|MP|，即|c-
|=整理得 因为c2-a2=b2，将其代入上式得a=b
所以e=
==故选C．
点评：本题主要考查了双曲线的简单性质．解题的关键是熟练掌握双曲线中渐近线、准线、焦距等基本知识．
练习册系列答案
相关题目
的右焦点为F，若过点F且倾斜角为
的直线与双曲线的右支有且只有一个交点，则双曲线离心率的取值范围是
的右焦点为F，右准线
与两条渐近线交于P，Q两点，如果
是直角三角形，则双曲线的离心率为 （
）
C．
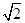D．
的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，与双曲线的其中一个交点为P，设O为坐标原点，若
，且
，则该双曲线的离心率为（ ）
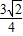
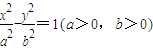的右焦点为F（c，0），方程ax2+bx-c=0的两实根分别为x1，x2，则P（x1，x2）（ ）