题目内容
对任意实数x，f（x）是x和x2-2中的较大者，则f（x）的最小值为 ．
【答案】分析：作出y=x和y=x2-2的图象，求出其交点坐标，确定出f（x）的解析式，再求其最小值．
解答：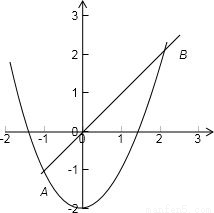
解：x=x2-2时，x=-1或x=2，由图象可知，
f（x）=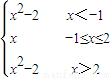
，故f（x）的最小值为-1
故答案为：-1．
点评：本题考查分段函数的最值问题，注意数形结合思想解题．
解答：
解：x=x2-2时，x=-1或x=2，由图象可知，f（x）=
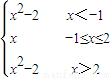，故f（x）的最小值为-1故答案为：-1．
点评：本题考查分段函数的最值问题，注意数形结合思想解题．
练习册系列答案
相关题目
设a，b，c是三角形ABC的边长，对任意实数x，f（x）=b2x2+（b2+c2-a2）x+c2有（ ）
| A、f（x）=0 | B、f（x）＞0 | C、f（x）≥0 | D、f（x）＜0 |