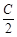Question

设a，b，c是三角形ABC的边长，对任意实数x，f（x）=b²x²+（b²+c²-a²）x+c²有（　　）

• A、f（x）=0
• B、f（x）＞0
• C、f（x）≥0
• D、f（x）＜0

Answer 1

分析：根据余弦定理a²=b²+c²-2bccosA的式子，将函数化简为f（x）=b²x²+（2bccosA）x+c²，再根据二次函数的图象与性质加以计算，可得函数图象对应的抛物线开口向上且与x轴没有公共点，可得本题的答案．

解答：解：在△ABC中，根据余弦定理a²=b²+c²-2bccosA，
∴b²+c²-a²=2bccosA，
因此函数可化为：f（x）=b²x²+（2bccosA）x+c²，
∵

b2＞0 △=4b2c2cos2A-4b2c2=4b2c2(cos2A-1)＜0

，
∴函数y=f（x）的图象是开口向上的抛物线，且与x轴没有公共点．
由此可得：对任意实数x，f（x）＞0恒成立．
故选：B

点评：本题给出与△ABC的三边a、b、c有关的二次函数，研究函数值的取值范围．着重考查了二次函数的图象与性质、余弦定理及其应用等知识，属于中档题．