题目内容
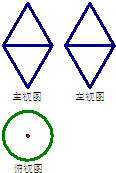一个空间几何体的主视图、左视图是周长为8，一个内角为60°的菱形，俯视图是圆及其圆心（如右图），那么这个几何体的体积为（ ）A、
| ||||
B、
| ||||
| C、2π | ||||
| D、4π |
分析：由三视图可得，几何体是由两个底面直径为2，母线长为2的圆锥组合而成，代入圆锥体积公式，即可求解．
解答：解：∵几何体的正视图、侧视图是周长为8一个内角为60°的菱形
∴几何体是由两个底面直径为2，母线长为2的圆锥组合而成，
∴V=2×
×π×1×
=
．
故选B．
∴几何体是由两个底面直径为2，母线长为2的圆锥组合而成，
∴V=2×
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
故选B．
点评：本题考查的知识点是由三视图求面积，其中根据已知条件判断几何体的形状及底面直径和母线的长是解答的关键．
练习册系列答案
相关题目
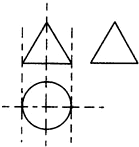如图，一个空间几何体的主视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么这个几何体的侧面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
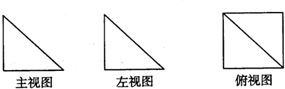下图是一个空间几何体的主视图（正视图），左视图、俯视图，如果直角三角形边长均为1，那么这个几何体的侧面积为（ ）A、2+2
| ||
B、1+2
| ||
C、2+
| ||
D、1+
|
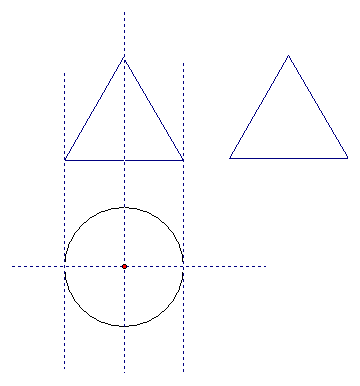
如图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，用一段铁丝从几何体的A处缠绕几何体两周到达B处，则铁丝的最短长度为