题目内容
 如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,用一段铁丝从几何体的A处缠绕几何体两周到达B处,则铁丝的最短长度为
如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,用一段铁丝从几何体的A处缠绕几何体两周到达B处,则铁丝的最短长度为分析:根据几何体的主视图、左视图都是边长为1的正方形,俯视图是一个直径为1的圆,得到几何体是一个圆柱,圆柱的底面直径是1,圆柱的高是1,铁丝在铁管上缠绕2圈,且铁丝的两个端点落在圆柱的同一母线的两端,则我们可以得到将圆柱面展开后得到的平面图形,然后根据平面上求两点间距离最小值的办法,即可求解.
解答: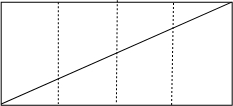 解:∵几何体的主视图、左视图都是边长为1的正方形,俯视图是一个直径为1的圆,
解:∵几何体的主视图、左视图都是边长为1的正方形,俯视图是一个直径为1的圆,
∴几何体是一个圆柱,
圆柱的底面直径是1,圆柱的高是1,
又∵铁丝在铁管上缠绕2圈,且铁丝的两个端点落在圆柱的同一母线的两端,
则我们可以得到将圆柱面展开后得到的平面图形,
其中每一个小矩形的宽为圆柱的周长πcm,高为圆柱的高1,
则大矩形的对称线即为铁丝的长度最小值.
此时铁丝的长度最小值为:
故答案为:
.
 解:∵几何体的主视图、左视图都是边长为1的正方形,俯视图是一个直径为1的圆,
解:∵几何体的主视图、左视图都是边长为1的正方形,俯视图是一个直径为1的圆,∴几何体是一个圆柱,
圆柱的底面直径是1,圆柱的高是1,
又∵铁丝在铁管上缠绕2圈,且铁丝的两个端点落在圆柱的同一母线的两端,
则我们可以得到将圆柱面展开后得到的平面图形,
其中每一个小矩形的宽为圆柱的周长πcm,高为圆柱的高1,
则大矩形的对称线即为铁丝的长度最小值.
此时铁丝的长度最小值为:
| 1+4π2 |
故答案为:
| 1+4π2 |
点评:本题考查由三视图求几何体的表面积,考查有三视图还原直观图,本题是一个基础题,题目的条件比较简单,是一个送分题目.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目

 己知一个空间几何体的三视图如图所示,其中正
己知一个空间几何体的三视图如图所示,其中正 (B)
(B)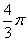
 (D)
(D)