题目内容
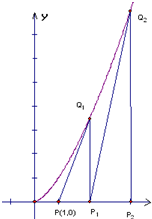 如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.(Ⅰ)试求数列{an}的通项公式an;(用k的代数式表示)
(Ⅱ)求证:an≥1+
| n |
| k-1 |
(Ⅲ)求证:
| n |
 |
| i=1 |
| i |
| ai |
| n |
 |
| i=1 |
分析:(Ⅰ)由曲线C:y=xk,求导得切线斜率,切点Qn的坐标(an,ank),得切线方程,切线过点Pn-1(an-1,0),代入方程,得关于数列{an}项的关系式,变形得出数列{an}为等比数列,可求数列{an}的通项公式;
(Ⅱ)把每一项的分子用错位相减法都化为1,然后用等比数列的前n项和求解.
(Ⅲ)先求出
的表达式,进而求得其前n项和的表达式,利用错位相减法即可证明
Sn<k-1,进而可以证明
<k2-k.
(Ⅱ)把每一项的分子用错位相减法都化为1,然后用等比数列的前n项和求解.
(Ⅲ)先求出
| i |
| ai |
| 1 |
| k |
| n |
 |
| i=1 |
| i |
| ai |
解答:解:(Ⅰ)∵y=xk
∴y'=kxk-1,若切点是Qn(an,ank),
则切线方程为y-ank=kank-1(x-an).
当n=1时,切线过点P(1,0),即0-a1k=ka1k-1(1-a1),得a1=
当n>1时,切线过点Pn-1(an-1,0),即0-ank=kank-1(an-1-an),解得
=
.
∴数列{an}是首项为
,公比为
的等比数列,
故所求通项an=(
)n,n∈N*.
(Ⅱ) 由(Ⅰ)知.
∴an=(
)n=(1+
)n=Cn0+Cn1
+Cn2(
)2+…+Cnn(
)n≥Cn0+Cn1
=1+
;
(Ⅲ)设Sn=
+
+…+
+
,
则
Sn=
+
+…+
+
,
两式相减得(1-
)Sn=
+
+…+
-
<
+
+…+
;
∴
Sn<
<k-1,
故Sn<k2-k.(14分)
∴y'=kxk-1,若切点是Qn(an,ank),
则切线方程为y-ank=kank-1(x-an).
当n=1时,切线过点P(1,0),即0-a1k=ka1k-1(1-a1),得a1=
| k |
| k-1 |
当n>1时,切线过点Pn-1(an-1,0),即0-ank=kank-1(an-1-an),解得
| an |
| an-1 |
| k |
| k-1 |
∴数列{an}是首项为
| k |
| k-1 |
| k |
| k-1 |
故所求通项an=(
| k |
| k-1 |
(Ⅱ) 由(Ⅰ)知.
∴an=(
| k |
| k-1 |
| 1 |
| k-1 |
| 1 |
| k-1 |
| 1 |
| k-1 |
| 1 |
| k-1 |
| 1 |
| k-1 |
| n |
| k-1 |
(Ⅲ)设Sn=
| 1 |
| a1 |
| 2 |
| a2 |
| n-1 |
| an-1 |
| n |
| an |
则
| k-1 |
| k |
| 1 |
| a2 |
| 2 |
| a3 |
| n-1 |
| an |
| n |
| an+1 |
两式相减得(1-
| k-1 |
| k |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| n |
| an+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
∴
| 1 |
| k |
| ||||
1-
|
故Sn<k2-k.(14分)
点评:本题主要考查数列、导数、不等式和数学归纳法等知识,考查化归与转化的数学思想方法,以及逻辑推理、抽象概括能力,运算求解能力和创新意识,此题有点难度,是各地高考的热点,需要同学们掌握.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
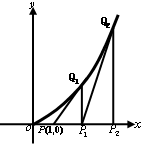 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.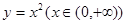 的切线,切点为
的切线,切点为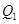 ,设点
,设点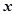 轴上的投影是点
轴上的投影是点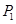 ;又过点
;又过点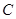 的切线,切点为
的切线,切点为 ,设
,设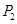 ;………;依此下去,得到一系列点
;………;依此下去,得到一系列点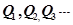
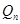 ,设点
,设点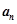 .
.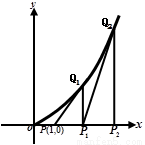
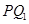 的方程;
的方程;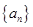 的通项公式;
的通项公式;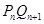 的距离为
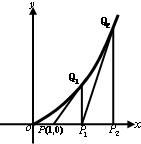
的距离为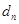 ,求证:
,求证: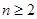 时,
时,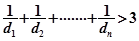
 如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.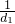 +
+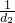 +…
+…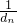 >3.
>3.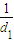 +
+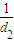 +…
+…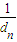 >3.
>3.