题目内容
在△ABC中，若三个内角A、B、C成等差数列，且b=2，则△ABC外接圆半径为 ．
【答案】分析：设外接圆的半径为 r，根据三个内角A、B、C成等差数列，求得B=60°，则由正弦定理可得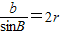 
，解方程求得r．
解答：解：∵三个内角A、B、C成等差数列'
∴2B=A+C，A+B+C=180°，
∴B=60°，
设外接圆的半径为 r，则由正弦定理可得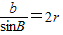
，
∴
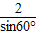=2r，∴r=
，
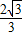故答案为：
．
点评：本题考查正弦定理的应用，得到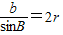
，是解题的关键，属中档题．
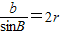，解方程求得r．解答：解：∵三个内角A、B、C成等差数列'
∴2B=A+C，A+B+C=180°，
∴B=60°，
设外接圆的半径为 r，则由正弦定理可得
，∴
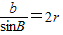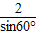=2r，∴r=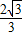，故答案为：
．点评：本题考查正弦定理的应用，得到
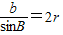，是解题的关键，属中档题． 
练习册系列答案
同步练习强化拓展系列答案
相关题目