题目内容
已知数列{ax}和{bx}满足: .且{bx}是以
.且{bx}是以a为公比的等比数列.
(Ⅰ)证明:aa+2=a1a2;
(Ⅱ)若a3n-1+2a2,证明数例{cx}是等比数例;
(Ⅲ)求和:
 …
… .
.
【答案】分析:(I)由 ,知
,知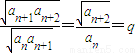 ,由此可得an+2=anq2(n∈N*).
,由此可得an+2=anq2(n∈N*).
(II)由题意知a2n-1=a1q2n-2,a2n=a2qn-2,所以cn=a2n-1+2a2n=5q2n-2.由此可知{cn}是首项为5,以q2为公比的等比数列.
(III)由题设条件得 ,
, ,所以
,所以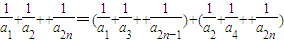 =
= .由此可知
.由此可知
解答:解:(I)证:由 ,有
,有 ,∴an+2=anq2(n∈N*).
,∴an+2=anq2(n∈N*).
(II)证:∵an=qn-2q2,∴a2n-1=a2n-3q2═a1q2n-2,a2n=a2n-2q2═a2qn-2,∴cn=a2n-1+2a2n=a1q2n-2+2a2q2n-2=(a1+2a2)q2n-2=5q2n-2.∴{cn}是首项为5,以q2为公比的等比数列.
(III)由(II)得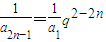 ,
,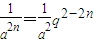 ,于是
,于是 =
= =
= .
.
当q=1时, =
=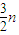 .
.
当q≠1时,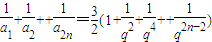 =
= =
=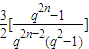 .
.
故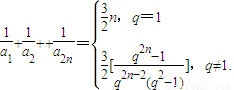
点评:本题主要考查等比数列的定义,通项公式和求和公式等基本知识及基本的运算技能,考查分析问题能力和推理能力.
 ,知
,知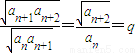 ,由此可得an+2=anq2(n∈N*).
,由此可得an+2=anq2(n∈N*).(II)由题意知a2n-1=a1q2n-2,a2n=a2qn-2,所以cn=a2n-1+2a2n=5q2n-2.由此可知{cn}是首项为5,以q2为公比的等比数列.
(III)由题设条件得
 ,
, ,所以
,所以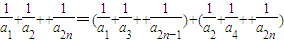 =
= .由此可知
.由此可知
解答:解:(I)证:由
 ,有
,有 ,∴an+2=anq2(n∈N*).
,∴an+2=anq2(n∈N*).(II)证:∵an=qn-2q2,∴a2n-1=a2n-3q2═a1q2n-2,a2n=a2n-2q2═a2qn-2,∴cn=a2n-1+2a2n=a1q2n-2+2a2q2n-2=(a1+2a2)q2n-2=5q2n-2.∴{cn}是首项为5,以q2为公比的等比数列.
(III)由(II)得
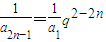 ,
,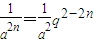 ,于是
,于是 =
= =
= .
.当q=1时,
 =
=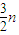 .
.当q≠1时,
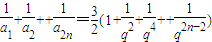 =
= =
=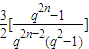 .
.故
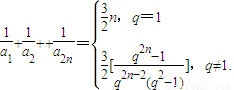
点评:本题主要考查等比数列的定义,通项公式和求和公式等基本知识及基本的运算技能,考查分析问题能力和推理能力.

练习册系列答案
相关题目
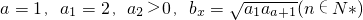 .且{bx}是以
.且{bx}是以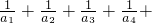 …
…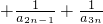 .
.