题目内容
对于函数f(x)=ex定义域中任意x1,x2(x1≠x2)有如下结论:
①f(x1+x2)=f(x1)•f(x2);
②f(x1•x2)=f(x1)+f(x2);
③ >0;
>0;
④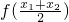 <
<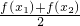 .
.
上述结论中正确的结论个数是
- A.1
- B.2
- C.3
- D.4
C
分析:由指数的运算性质可判断①与②的真假,根据函数的单调性可以判断③的正误,根据函数图象的形状可以判断④的对错,进而得到答案.
解答:∵f(x)=ex
∴f(x1+x2)=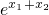 =
= •
• =f(x1)•f(x2),故①正确;
=f(x1)•f(x2),故①正确;
∵f(x1•x2)= ;f(x1)+f(x2)=
;f(x1)+f(x2)= +
+ ,故②错误;
,故②错误;
∵e>1,故函数f(x)=ex为增函数,故 >0成立,即③正确;
>0成立,即③正确;
而函数f(x)=ex图象为凹形上升的,故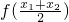 <
<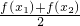 ,故④正确.
,故④正确.
故上述四个结论中有3个结论是正确的
故选C
点评:本题考查的知识点是指数的运算性质,指数函数的单调性,指数函数图象的形状,正确的理解结论中式子所表示的含义是解答本题的关键.
分析:由指数的运算性质可判断①与②的真假,根据函数的单调性可以判断③的正误,根据函数图象的形状可以判断④的对错,进而得到答案.
解答:∵f(x)=ex
∴f(x1+x2)=
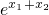 =
= •
• =f(x1)•f(x2),故①正确;
=f(x1)•f(x2),故①正确;∵f(x1•x2)=
 ;f(x1)+f(x2)=
;f(x1)+f(x2)= +
+ ,故②错误;
,故②错误;∵e>1,故函数f(x)=ex为增函数,故
 >0成立,即③正确;
>0成立,即③正确;而函数f(x)=ex图象为凹形上升的,故
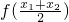 <
<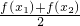 ,故④正确.
,故④正确.故上述四个结论中有3个结论是正确的
故选C
点评:本题考查的知识点是指数的运算性质,指数函数的单调性,指数函数图象的形状,正确的理解结论中式子所表示的含义是解答本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
对于函数f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“可构造三角形函数”.以下说法正确的是( )
| A、f(x)=1(x∈R)不是“可构造三角形函数” | ||
| B、“可构造三角形函数”一定是单调函数 | ||
C、f(x)=
| ||
D、若定义在R上的函数f(x)的值域是[
|