题目内容
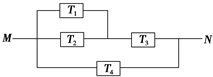 如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知
T1,T2,T3中至少有一个能通过电流的概率为0.999.
(1)求p;
(2)求电流能在M与N之间通过的概率;
(3)ξ表示T1,T2,T3,T4中能通过电流的元件个数,求ξ的期望.
分析:记Ai表示事件:电流能通过Ti,i=1、2、3、4,A表示事件:T1,T2,T3中至少有一个能通过电流,B表示事件:电流能在M、N之间通过.
(I)T1,T2,T3中至少有一个能通过电流的概率为0.999,可得它们都不能通过电流的概率为1-0.999=0.001.由于Ai之间相互独立且发生的概率均为p,可得P(
)=P(
)P(
)P(
)=(1-p)3=0.001,解之得p=0.9;
(II)将B分解为A4、
A1A3与
A2A3的和,再用概率的乘法公式和加法公式,可求出电流能在M与N之间通过的概率;
(III)由题意可得:ξ服从二项分布,n=4且p=0.9.利用二项分布的数学期望公式,可以算出求ξ的期望.
(I)T1,T2,T3中至少有一个能通过电流的概率为0.999,可得它们都不能通过电流的概率为1-0.999=0.001.由于Ai之间相互独立且发生的概率均为p,可得P(
. |
| A |
. |
| A1 |
. |
| A2 |
. |
| A3 |
(II)将B分解为A4、
. |
| A4 |
. |
| A4 |
. |
| A1 |
(III)由题意可得:ξ服从二项分布,n=4且p=0.9.利用二项分布的数学期望公式,可以算出求ξ的期望.
解答:解:记Ai表示事件:电流能通过Ti,i=1、2、3、4,
A表示事件:T1,T2,T3中至少有一个能通过电流,
B表示事件:电流能在M、N之间通过.
(I)
=
•
•
,(A1,A2,A3相互独立)
∴P(
)=P(
•
•
)=P(
)P(
)P(
)=(1-p)3,
又∵P(
)=1-P(A)=1-0.999=0.001
∴(1-p)3=0.001,解之得p=0.9
(II)∵B=A4+
•A1•A3+
•
•A2•A3,
∴P(B)=P(A4)+P(
•A1•A3)+P(
•
•A2•A3)
=P(A4)+P(
)P(A1)P(A3)+P(
)P(
)P(A2)P(A3)
=0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9=0.9891
即电流能在M与N之间通过的概率为0.991
(III)由于电流能通过各元件的概率都是0.9,且电流能通过各元件相互独立,
用ξ表示T1,T2,T3,T4中能通过电流的元件个数,则ξ服从二项分布,n=4且p=0.9
即ξ~B(4,0.9),由二项分布的数学期望公式,得Eξ=4×0.9=3.6
即ξ的期望为3.6
A表示事件:T1,T2,T3中至少有一个能通过电流,
B表示事件:电流能在M、N之间通过.
(I)
. |
| A |
. |
| A1 |
. |
| A2 |
. |
| A3 |
∴P(
. |
| A |
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
又∵P(
. |
| A |
∴(1-p)3=0.001,解之得p=0.9
(II)∵B=A4+
. |
| A4 |
. |
| A4 |
. |
| A1 |
∴P(B)=P(A4)+P(
. |
| A4 |
. |
| A4 |
. |
| A1 |
=P(A4)+P(
. |
| A4 |
. |
| A4 |
. |
| A1 |
=0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9=0.9891
即电流能在M与N之间通过的概率为0.991
(III)由于电流能通过各元件的概率都是0.9,且电流能通过各元件相互独立,
用ξ表示T1,T2,T3,T4中能通过电流的元件个数,则ξ服从二项分布,n=4且p=0.9
即ξ~B(4,0.9),由二项分布的数学期望公式,得Eξ=4×0.9=3.6
即ξ的期望为3.6
点评:本题给出一个并联和串联相复合的电路,求电流能接通的概率,着重考查了相互独立事件的概率乘法公式、互斥事件与对立事件和离散型随机变量的期望与方差等知识,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
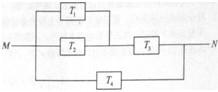 如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是P,电流能通过T4的概率是0.9,电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是P,电流能通过T4的概率是0.9,电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.

