题目内容
复平面内有A、B、C三点,点A对应复数是3+i,向量 对应复数是-2-4i,向量
对应复数是-2-4i,向量 表示的复数是-4-i,求B点对应复数.
表示的复数是-4-i,求B点对应复数.
 对应复数是-2-4i,向量
对应复数是-2-4i,向量 表示的复数是-4-i,求B点对应复数.
表示的复数是-4-i,求B点对应复数. ∵ 表示的复数是2+4i,
表示的复数是2+4i, 表示的复数是4+i,
表示的复数是4+i,
∴ 表示的复数为(4+i)-(2+4i)=2-3i,
表示的复数为(4+i)-(2+4i)=2-3i,
故 =
= +
+ 对应的复数为(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i.
对应的复数为(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i.
 表示的复数是2+4i,
表示的复数是2+4i, 表示的复数是4+i,
表示的复数是4+i,∴
 表示的复数为(4+i)-(2+4i)=2-3i,
表示的复数为(4+i)-(2+4i)=2-3i,故
 =
= +
+ 对应的复数为(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i.
对应的复数为(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i.本试题主要考查了复数的几何意义的运用。首先利用向量与点一一对应以及复数与向量一一对应的特点可知,∵ 表示的复数是2+4i,
表示的复数是2+4i, 表示的复数是4+i,
表示的复数是4+i,
∴ 表示的复数为(4+i)-(2+4i)=2-3i,故
表示的复数为(4+i)-(2+4i)=2-3i,故 =
= +
+ 对应的复数为
对应的复数为
(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i得到结论。
解: ∵ 表示的复数是2+4i,
表示的复数是2+4i, 表示的复数是4+i,
表示的复数是4+i,
∴ 表示的复数为(4+i)-(2+4i)=2-3i,故
表示的复数为(4+i)-(2+4i)=2-3i,故 =
= +
+ 对应的复数为
对应的复数为
(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i.
 表示的复数是2+4i,
表示的复数是2+4i, 表示的复数是4+i,
表示的复数是4+i,∴
 表示的复数为(4+i)-(2+4i)=2-3i,故
表示的复数为(4+i)-(2+4i)=2-3i,故 =
= +
+ 对应的复数为
对应的复数为(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i得到结论。
解: ∵
 表示的复数是2+4i,
表示的复数是2+4i, 表示的复数是4+i,
表示的复数是4+i,∴
 表示的复数为(4+i)-(2+4i)=2-3i,故
表示的复数为(4+i)-(2+4i)=2-3i,故 =
= +
+ 对应的复数为
对应的复数为(3+i)+(2-3i)=5-2i,∴B点对应的复数为zB=5-2i.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
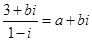 (
(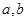 为实数,
为实数,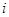 为虚数单位),则
为虚数单位),则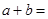 __________
__________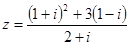 ,若
,若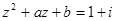 ,求实数
,求实数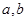 的值。
的值。 ,则复数
,则复数 等于( )
等于( )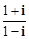 )2010,则z=_______ ___.
)2010,则z=_______ ___.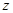 的共轭复数为
的共轭复数为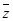 ,若
,若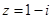 (
(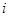 为虚数单位)则
为虚数单位)则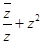 的值为_______.
的值为_______.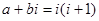 (其中
(其中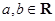 ,
,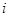 是虚数单位),则
是虚数单位),则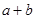 的值为( )
的值为( )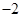
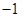
 的共轭复数是( )。
的共轭复数是( )。



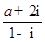 在复平面内所对应的点在虚轴上,那么实数
在复平面内所对应的点在虚轴上,那么实数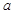 = .
= .