题目内容
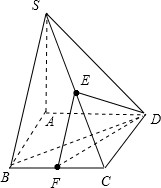
 如图,四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,点E是SC的中点,SA=4,AB=2.
如图,四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,点E是SC的中点,SA=4,AB=2.(理)(1)求直线ED与直线SB所成的角;
(2)求点A到平面SBD的距离.
(文)(1)求直线SC与平面SAD所成的角;
(2)求直线ED与直线SB所成的角.
分析:(理)(1)取BC的中点为F,连接EF、DF,可得EF∥SB,即可得到∠FED为所求,再利用解三角形的有关知识求出答案即可.
(2)设点A到平面SBD的距离为h,根据题中的条件可得S△SBD=6,S△ABD=2,再根据VA-BDS=VS-ABD,可得点A到平面SBD的距离.
(文)(1)由题意可得:CD⊥AD,又因为SA⊥面ABCD,所以AD⊥SA,所以CD⊥平面SAD,所以∠CSD为所求,再利用解三角形的有关知识求出答案.
(2)取BC的中点为F,连接EF、DF,可得EF∥SB,即可得到∠FED为所求,再利用解三角形的有关知识求出答案即可.
(2)设点A到平面SBD的距离为h,根据题中的条件可得S△SBD=6,S△ABD=2,再根据VA-BDS=VS-ABD,可得点A到平面SBD的距离.
(文)(1)由题意可得:CD⊥AD,又因为SA⊥面ABCD,所以AD⊥SA,所以CD⊥平面SAD,所以∠CSD为所求,再利用解三角形的有关知识求出答案.
(2)取BC的中点为F,连接EF、DF,可得EF∥SB,即可得到∠FED为所求,再利用解三角形的有关知识求出答案即可.
解答:(理)解:(1)取BC的中点为F,连接EF、DF,
因为点E是SC的中点,
所以EF∥SB,所以“直线ED与直线SB所成的角”与“直线ED与直线EF所成的角”相等或者互补,即∠FED为所求.
因为SA⊥面ABCD,SA=4,AB=2,
所以SB=2
,所以EF=
.
又因为ABCD是正方形,并且AB=2,
所以DF=
.
因为四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,
所以CD⊥平面SAD,所以CD⊥SD,所以ED=
,
因为ABCD是正方形,并且AB=2,SA=4,
所以SC=2
,所以ED=
.
在△EFD中,由余弦定理可得:cos∠FED=
,
所以直线ED与直线SB所成的角为arccos
.
(2)设点A到平面SBD的距离为h,
因为SA⊥面ABCD,SA=4,AB=2,
所以SB=SD=2
,
因为ABCD是正方形,并且AB=2,
所以BD=2
,所以S△SBD=6,S△ABD=2,
因为VA-BDS=VS-ABD,
所以
×S△SBD×h=
×S△ABD×|SA|,解得:h=
,
所以点A到平面SBD的距离为
.
(文)解:(1)因为四棱锥S-ABCD的底面是正方形,
所以CD⊥AD,
又因为SA⊥面ABCD,即AD⊥SA,
因为AD∩SA=A,
所以CD⊥平面SAD,
所以∠CSD为所求.
因为四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,SA=4,AB=2.
所以CD=2,SD=2
,
所以tan∠CSD=
=
,
所以直线SC与平面SAD所成的角为arctan
.
(2)取BC的中点为F,连接EF、DF,
因为点E是SC的中点,
所以EF∥SB,所以“直线ED与直线SB所成的角”与“直线ED与直线EF所成的角”相等或者互补,即∠FED为所求.
因为SA⊥面ABCD,SA=4,AB=2,
所以SB=2
,所以EF=
.

又因为ABCD是正方形,并且AB=2,
所以DF=
.
因为四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,
所以CD⊥平面SAD,所以CD⊥SD,所以ED=
,
因为ABCD是正方形,并且AB=2,SA=4,
所以SC=2
,所以ED=
.
在△EFD中,由余弦定理可得:cos∠FED=
,
所以直线ED与直线SB所成的角为arccos
.
因为点E是SC的中点,
所以EF∥SB,所以“直线ED与直线SB所成的角”与“直线ED与直线EF所成的角”相等或者互补,即∠FED为所求.
因为SA⊥面ABCD,SA=4,AB=2,

所以SB=2
| 5 |
| 5 |
又因为ABCD是正方形,并且AB=2,
所以DF=
| 5 |
因为四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,
所以CD⊥平面SAD,所以CD⊥SD,所以ED=
| SC |
| 2 |
因为ABCD是正方形,并且AB=2,SA=4,
所以SC=2
| 6 |
| 6 |
在△EFD中,由余弦定理可得:cos∠FED=
| ||
| 10 |
所以直线ED与直线SB所成的角为arccos
| ||
| 10 |
(2)设点A到平面SBD的距离为h,
因为SA⊥面ABCD,SA=4,AB=2,
所以SB=SD=2
| 5 |
因为ABCD是正方形,并且AB=2,
所以BD=2
| 2 |
因为VA-BDS=VS-ABD,
所以
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
所以点A到平面SBD的距离为
| 4 |
| 3 |
(文)解:(1)因为四棱锥S-ABCD的底面是正方形,
所以CD⊥AD,
又因为SA⊥面ABCD,即AD⊥SA,
因为AD∩SA=A,
所以CD⊥平面SAD,
所以∠CSD为所求.
因为四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,SA=4,AB=2.
所以CD=2,SD=2
| 5 |
所以tan∠CSD=
| |SD| |
| |CD| |
| 5 |
所以直线SC与平面SAD所成的角为arctan
| 5 |
(2)取BC的中点为F,连接EF、DF,
因为点E是SC的中点,
所以EF∥SB,所以“直线ED与直线SB所成的角”与“直线ED与直线EF所成的角”相等或者互补,即∠FED为所求.
因为SA⊥面ABCD,SA=4,AB=2,
所以SB=2
| 5 |
| 5 |

又因为ABCD是正方形,并且AB=2,
所以DF=
| 5 |
因为四棱锥S-ABCD的底面是正方形,SA⊥面ABCD,
所以CD⊥平面SAD,所以CD⊥SD,所以ED=
| SC |
| 2 |
因为ABCD是正方形,并且AB=2,SA=4,
所以SC=2
| 6 |
| 6 |
在△EFD中,由余弦定理可得:cos∠FED=
| ||
| 10 |
所以直线ED与直线SB所成的角为arccos
| ||
| 10 |
点评:本题主要考查线线角与线面角,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键;而求点到平面的距离,一般运用等体积法进行求解.也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角、空间距离以及判断空间中的点线面的位置等问题.

练习册系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.