题目内容
下面有四个命题:
①函数y=sin4x-cos4x的最小正周期是π.
②终边在直线y=±x上的角的集合是{α|α=
+
,k∈Z}
③函数y=sin(x-
)在[0,π]上是减函数.
④连续函数f(x)定义在[2,4]上,若有f(2)•f(4)<0,要用二分法求f(x)的一个零点,精确度为0.1,则最多将进行5次二等分区间.
其中,真命题的编号是
①函数y=sin4x-cos4x的最小正周期是π.
②终边在直线y=±x上的角的集合是{α|α=
| kπ |
| 2 |
| π |
| 4 |
③函数y=sin(x-
| π |
| 2 |
④连续函数f(x)定义在[2,4]上,若有f(2)•f(4)<0,要用二分法求f(x)的一个零点,精确度为0.1,则最多将进行5次二等分区间.
其中,真命题的编号是
①②④
①②④
(写出所有真命题的编号)分析:①先化简,利用周期公式判断.②根据角的终边定义判断.③利用三角函数的图象平移关系判断.④利用三角函数的图象和性质判断.⑤利用二分法的定义进行判断.
解答:解:①y=sin4x-cos4x=y=(sin2x-cos2x)(sin2x+cos2x)=sin2x-cos2x=-cos2x,周期T=
=π,所以①正确.
②终边在直线y=±x上的角的集合是{α|α=
+
,k∈Z},所以②正确.
③y=sin?(x-
)=-cos?x,所以在[0,π]函数单调递增,所以③错误.
④连续函数f(x)定义在[2,4]上,若有f(2)•f(4)>0,要用二分法求f(x)的一个零点,精确度为0.1,则最多将进行5次二等分区间,所以④正确.
故答案为:①②④.
| 2π |
| 2 |
②终边在直线y=±x上的角的集合是{α|α=
| kπ |
| 2 |
| π |
| 4 |
③y=sin?(x-
| π |
| 2 |
④连续函数f(x)定义在[2,4]上,若有f(2)•f(4)>0,要用二分法求f(x)的一个零点,精确度为0.1,则最多将进行5次二等分区间,所以④正确.
故答案为:①②④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
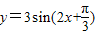 的图象向右平移
的图象向右平移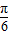 得y=3sin2x的图象;
得y=3sin2x的图象;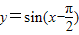 在(0,π)上是减函数.
在(0,π)上是减函数.