题目内容
某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为g(x)万元(总成本=固定成本+生产成本),并且销售收人r(x)满足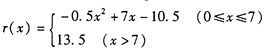
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
(1)大于300台小于1050台; (2) 600台
解析试题分析:(1) 由于销售收入是一个关于产品数量x的一个分段函数,另外计算工厂的盈利需要将销售收入r(x)减去总的成本g(x)万元,所以在两段函数中分别求出盈利大于零的时候产品数量的范围,及可求得结论.
(2)通过二次函数的最值的求法即可得到盈利最大值时对应的产品数x的值,本小题单位的转化也是易错点.
试题解析:依题意得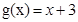 ,设利润函数为
,设利润函数为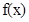 ,则
,则 ,
,
所以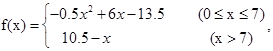 (1)要使工厂有盈利,则有f(x)>0,因为
(1)要使工厂有盈利,则有f(x)>0,因为
f(x)>0?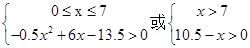 ,
,
⇒ ⇒
⇒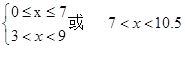
⇒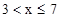 或
或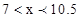 , 即
, 即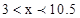 .
.
所以要使工厂盈利,产品数量应控制在大于300台小于1050台的范围内
(2)当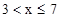 时,
时, 
故当x=6时,f(x)有最大值4.5.而当x>7时,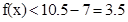 .
.
所以当工厂生产600台产品时,盈利最大.
考点:1.分段函数的应用.2.函数的最值.3.实际问题的构建数学模型解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①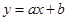 ;②
;②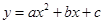 ;③
;③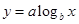 .
.(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格.

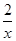 +
+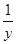 =
=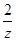 ;
; 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.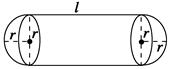
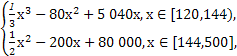
 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为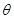 (弧度).
(弧度).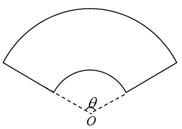
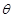 关于
关于 ,求
,求 的函数关系式,并求出
的函数关系式,并求出