题目内容
三个同学对问题“关于x的不等式x2+25+|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路.甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于x的函数,作出函数图象”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是
分析:利用“不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”的想法:原式化为:a≤x+
+|x2-5x|
再利用:“只须不等式左边的最小值不小于右边的最大值”即可解决.
| 25 |
| x |
再利用:“只须不等式左边的最小值不小于右边的最大值”即可解决.
解答:解:由x2+25+|x3-5x2|≥ax,1≤x≤12?a≤x+
+|x2-5x|,
而x+
≥2
=10,等号当且仅当x=5∈[1,12]时成立;
且|x2-5x|≥0,等号当且仅当x=5∈[1,12]时成立;
所以,a≤[x+
+|x2-5x|]min=10,等号当且仅当x=5∈[1,12]时成立;
故答案为(-∞,10];
| 25 |
| x |
而x+
| 25 |
| x |
x•
|
且|x2-5x|≥0,等号当且仅当x=5∈[1,12]时成立;
所以,a≤[x+
| 25 |
| x |
故答案为(-∞,10];
点评:本题主要考查了绝对值不等式的解法、基本不等式在最值问题中的应用,是一道已给出解法提示,让解题者得到友情提醒的情况下答题,富有创意.

练习册系列答案
相关题目
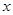 的不等式
的不等式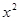 +25+|
+25+|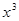 -5
-5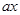 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数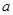 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路. 的不等式
的不等式 +25+|
+25+| -5
-5 在[1,12]上恒成
在[1,12]上恒成 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.