题目内容
某公园准备建一个摩天轮,摩天轮的外围是一个周长为K米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为12K元/根,且当两相邻的座位之间的圆弧长为X米时,相邻两座位之间的钢管和其中一个座位的总费用为[
+8]K元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为Y元.
(Ⅰ)试写出Y关于X的函数关系式,并写出定义域;
(Ⅱ)当K=100米时,试确定座位的个数,使得总造价最低?
| (512X2+20)X | 100 |
(Ⅰ)试写出Y关于X的函数关系式,并写出定义域;
(Ⅱ)当K=100米时,试确定座位的个数,使得总造价最低?
分析:(Ⅰ)由题意,总造价y中包括座位和圆心处的支点间的钢管的费用,相邻座位之间的钢管与座位的费用,故只需算出座位的个数即知钢管的个数,将两项费用表示出来,相加即得y关于x的函数关系式;
(Ⅱ)将k=100米代入函数关系式,利用导数求出最值即得最低的总造价.
(Ⅱ)将k=100米代入函数关系式,利用导数求出最值即得最低的总造价.
解答:解:(Ⅰ)设摩天轮上总共有n个座位,则x=
,即n=
,
∴y=12k×
+
[
+8]k=k2(
+
),
定义域{x|0<x≤
,
∈Z};(6分)
(Ⅱ)当k=100时,0<x≤25,令y=100(
+512x2+20)
f(x)=
+512x2,则f′(x)=-
+1024x=0,
∴x3=
,∴x=
,(10分)
当x∈(0,
)时,f′(x)<0,即f(x)在x∈(0,
)上单调减,
当x∈(
,25)时,f′(x)>0,即f(x)在x∈(
,25)上单调增,
∴ymin在x=
时取到,此时座位个数为
=80个.(15分)
| k |
| n |
| k |
| x |
∴y=12k×
| k |
| x |
| k |
| x |
| (512x2+20)x |
| 100 |
| 20 |
| x |
| 512x2+20 |
| 100 |
定义域{x|0<x≤
| k |
| 4 |
| k |
| x |
(Ⅱ)当k=100时,0<x≤25,令y=100(
| 2000 |
| x |
f(x)=
| 2000 |
| x |
| 2000 |
| x2 |
∴x3=
| 1000 |
| 512 |
| 5 |
| 4 |
当x∈(0,
| 5 |
| 4 |
| 5 |
| 4 |
当x∈(
| 5 |
| 4 |
| 5 |
| 4 |
∴ymin在x=
| 5 |
| 4 |
| 100 | ||
|
点评:本题考查利用导数解决现实中造价最优的一个应用题,解题的关键是正确构建函数,在求最值时要根据函数的形式选择合适的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为 元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元. 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低? 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为 元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.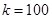 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?