题目内容
函数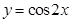 在点
在点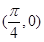 处的切线方程是( )
处的切线方程是( )
A.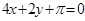 | B.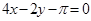 | C.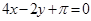 | D.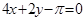 |
D
解析试题分析:因为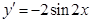 ,所求切线的斜率为
,所求切线的斜率为 ,所求的切线方程为
,所求的切线方程为 即
即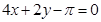 ,故选D.
,故选D.
考点:导数的几何意义.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
函数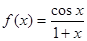 在
在 处的切线方程是( )
处的切线方程是( )
A.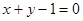 | B.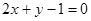 |
C. | D.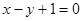 |
函数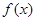 的定义域为开区间
的定义域为开区间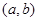 ,导函数
,导函数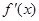 在
在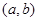 内的图象如图所示,则函数
内的图象如图所示,则函数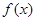 在开区间
在开区间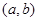 内有极小值点( )
内有极小值点( )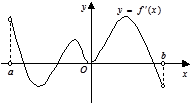
A.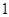 个 个 | B.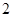 个 个 | C. 个 个 | D.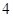 个 个 |
已知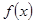 为定义在(-
为定义在(-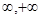 )上的可导函数,
)上的可导函数,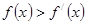 对于
对于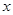 ∈R恒成立,且e为自然对数的底数,则( )
∈R恒成立,且e为自然对数的底数,则( )
A.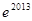 . .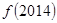 < < . .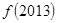 |
B.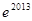 . .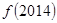 = = . .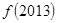 |
C.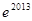 . .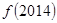 > > . .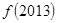 |
D.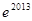 . .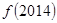 与 与 . .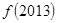 大小不确定 大小不确定 |
函数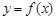 在点(x0,y0)处的切线方程为
在点(x0,y0)处的切线方程为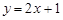 ,则
,则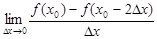 等于( )
等于( )
| A.-4 | B.-2 | C.2 | D.4 |
若函数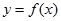 在区间
在区间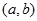 内可导,且
内可导,且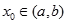 ,则
,则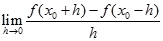
的值为( )
A.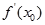 | B.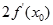 | C. | D.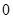 |
观察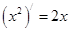 ,
,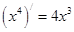 ,
,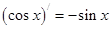 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在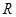 上的函数
上的函数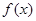 满足
满足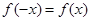 ,记
,记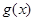 为
为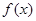 的导函数,则
的导函数,则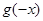 =( )
=( )
A.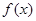 | B.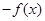 | C.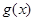 | D.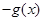 |
当 时,不等式
时,不等式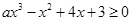 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. | B. | C. | D. |
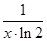 ;③(ex)′=ex;④(
;③(ex)′=ex;④(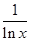 )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.