题目内容
已知函数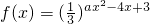
(1)若a=-1,求f(x)的单调区间;
(2)若f(x)有最大值3,求a的值.
解:(1)a=-1,得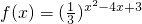 ,
,
∵ ∈(0,1),t=x2-4x+3的减区间为(-∞,2),增区间为(2,+∞)
∈(0,1),t=x2-4x+3的减区间为(-∞,2),增区间为(2,+∞)
∴f(x)的增区间为(-∞,2),减区间为(2,+∞)
(2)∵f(x)有最大值, ∈(0,1),
∈(0,1),
∴函数t=ax2-4x+3在区间(-∞, )上是增函数,在区间(
)上是增函数,在区间( ,+∞)上是减函数
,+∞)上是减函数
由此可得,a>0且f( )=
)=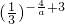 =3,得-
=3,得- +3=-1,解之得a=1
+3=-1,解之得a=1
综上所述,当f(x)有最大值3时,a的值为1
分析:(1)a=-1,因为 ∈(0,1),根据指数函数的单调性,得t=x2-4x+3的减区间就是f(x)的增区间,增区间就是f(x)的减区间,由此结合二次函数的单调性,不难得出f(x)的单调区间;
∈(0,1),根据指数函数的单调性,得t=x2-4x+3的减区间就是f(x)的增区间,增区间就是f(x)的减区间,由此结合二次函数的单调性,不难得出f(x)的单调区间;
(2)根据题意,得t=ax2-4x+3在区间(-∞, )上是增函数,在区间(
)上是增函数,在区间( ,+∞)上是减函数,从而得到a>0且f(x)的最大值为f(
,+∞)上是减函数,从而得到a>0且f(x)的最大值为f( )=3,解之得a=1.
)=3,解之得a=1.
点评:本题给出指数型复合函数,讨论函数的单调区间并求函数的最值,着重考查了指数函数的单调性和二次函数的图象与性质等知识,属于基础题.
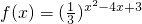 ,
,∵
 ∈(0,1),t=x2-4x+3的减区间为(-∞,2),增区间为(2,+∞)
∈(0,1),t=x2-4x+3的减区间为(-∞,2),增区间为(2,+∞)∴f(x)的增区间为(-∞,2),减区间为(2,+∞)
(2)∵f(x)有最大值,
 ∈(0,1),
∈(0,1),∴函数t=ax2-4x+3在区间(-∞,
 )上是增函数,在区间(
)上是增函数,在区间( ,+∞)上是减函数
,+∞)上是减函数由此可得,a>0且f(
 )=
)=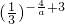 =3,得-
=3,得- +3=-1,解之得a=1
+3=-1,解之得a=1综上所述,当f(x)有最大值3时,a的值为1
分析:(1)a=-1,因为
 ∈(0,1),根据指数函数的单调性,得t=x2-4x+3的减区间就是f(x)的增区间,增区间就是f(x)的减区间,由此结合二次函数的单调性,不难得出f(x)的单调区间;
∈(0,1),根据指数函数的单调性,得t=x2-4x+3的减区间就是f(x)的增区间,增区间就是f(x)的减区间,由此结合二次函数的单调性,不难得出f(x)的单调区间; (2)根据题意,得t=ax2-4x+3在区间(-∞,
 )上是增函数,在区间(
)上是增函数,在区间( ,+∞)上是减函数,从而得到a>0且f(x)的最大值为f(
,+∞)上是减函数,从而得到a>0且f(x)的最大值为f( )=3,解之得a=1.
)=3,解之得a=1.点评:本题给出指数型复合函数,讨论函数的单调区间并求函数的最值,着重考查了指数函数的单调性和二次函数的图象与性质等知识,属于基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目

 ,求f(x)的解析式.
,求f(x)的解析式.
 ,求f(x)的解析式.
,求f(x)的解析式.