题目内容
已知函数
(1)若a=-4,求函数f(x)的单调性;
(2)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围;
(3)记函数g(x)=x2f′(x),若g(x)的最小值是
 ,求f(x)的解析式.
,求f(x)的解析式.
【答案】分析:(1)将a=-4代入函数的解析式,先求函数的定义域,求出函数的导函数,分析导函数符号在不同区间上的取值,根据导函数符号与原函数的单调性之间的关系可得结论;
(2)函数f(x)在[1,+∞)上单调递增,f′(x)≥0在[1,+∞)上恒成立,即a≥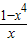 在[1,+∞)上恒成立,构造函数h(x)=
在[1,+∞)上恒成立,构造函数h(x)=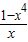 并求出其最小值,可得实数a的取值范围;
并求出其最小值,可得实数a的取值范围;
(3)g(x)=x2f′(x)=2x3+ax-2的最小值是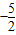 ,由此构造关于a的方程,解方程求出a值,可得f(x)的解析式.
,由此构造关于a的方程,解方程求出a值,可得f(x)的解析式.
解答:解:(1)当a=-4时,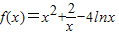 ,(x>0)
,(x>0)
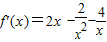 =
=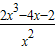 =
=
令f′(x)=0,则x=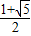
∵x∈(0,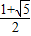 )时,f′(x)<0,∵当x∈(
)时,f′(x)<0,∵当x∈(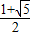 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,
∴(0,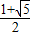 )为函数
)为函数 的单调递减区间,
的单调递减区间,
∴(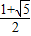 ,+∞)为函数
,+∞)为函数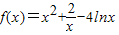 的单调递增区间;
的单调递增区间;
(2)∵f′(x)=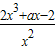
若函数f(x)在[1,+∞)上单调递增,
则f′(x)≥0在[1,+∞)上恒成立
即2x3+ax-2≥0在[1,+∞)上恒成立
即a≥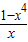 在[1,+∞)上恒成立
在[1,+∞)上恒成立
令h(x)=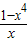 ,则h′(x)=
,则h′(x)= <0恒成立
<0恒成立
故h(x)=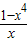 在[1,+∞)上单调递减
在[1,+∞)上单调递减
当x=1时,h(x)取最大值0
故a≥0,即实数a的取值范围为[0,+∞)
(3)g(x)=x2f′(x)=2x3+ax-2
则g′(x)=6x2+a,
当a≥0时,g′(x)≥0恒成立
此时g(x)在定义域(0,+∞)上无最小值
当a<0时,令g′(x)=6x2+a=0
则x=
∵x∈(0,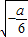 )时,f′(x)<0,∵当x∈(
)时,f′(x)<0,∵当x∈(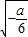 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,
∴(0,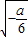 )为函数g(x)的单调递减区间,
)为函数g(x)的单调递减区间,
∴(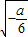 ,+∞)为函数g(x)的单调递增区间;
,+∞)为函数g(x)的单调递增区间;
当x=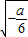 时,g(x)的最小值g(
时,g(x)的最小值g( )=
)=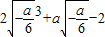 =
=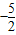 ,
,
解得a=-
∴
点评:本题考查的知识点是利用导数研究函数的单调性,函数解析式的求解及常用方法,其中熟练掌握导函数符号与原函数的单调性之间的关系,并又此分析函数的单调区间和极值点是解答的关键.
(2)函数f(x)在[1,+∞)上单调递增,f′(x)≥0在[1,+∞)上恒成立,即a≥
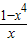 在[1,+∞)上恒成立,构造函数h(x)=
在[1,+∞)上恒成立,构造函数h(x)=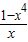 并求出其最小值,可得实数a的取值范围;
并求出其最小值,可得实数a的取值范围;(3)g(x)=x2f′(x)=2x3+ax-2的最小值是
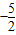 ,由此构造关于a的方程,解方程求出a值,可得f(x)的解析式.
,由此构造关于a的方程,解方程求出a值,可得f(x)的解析式.解答:解:(1)当a=-4时,
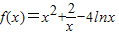 ,(x>0)
,(x>0)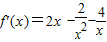 =
=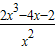 =
=
令f′(x)=0,则x=
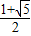
∵x∈(0,
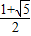 )时,f′(x)<0,∵当x∈(
)时,f′(x)<0,∵当x∈(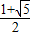 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,∴(0,
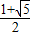 )为函数
)为函数 的单调递减区间,
的单调递减区间,∴(
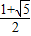 ,+∞)为函数
,+∞)为函数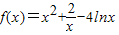 的单调递增区间;
的单调递增区间;(2)∵f′(x)=
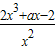
若函数f(x)在[1,+∞)上单调递增,
则f′(x)≥0在[1,+∞)上恒成立
即2x3+ax-2≥0在[1,+∞)上恒成立
即a≥
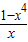 在[1,+∞)上恒成立
在[1,+∞)上恒成立令h(x)=
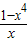 ,则h′(x)=
,则h′(x)= <0恒成立
<0恒成立故h(x)=
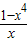 在[1,+∞)上单调递减
在[1,+∞)上单调递减当x=1时,h(x)取最大值0
故a≥0,即实数a的取值范围为[0,+∞)
(3)g(x)=x2f′(x)=2x3+ax-2
则g′(x)=6x2+a,
当a≥0时,g′(x)≥0恒成立
此时g(x)在定义域(0,+∞)上无最小值
当a<0时,令g′(x)=6x2+a=0
则x=

∵x∈(0,
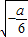 )时,f′(x)<0,∵当x∈(
)时,f′(x)<0,∵当x∈(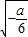 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,∴(0,
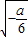 )为函数g(x)的单调递减区间,
)为函数g(x)的单调递减区间,∴(
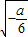 ,+∞)为函数g(x)的单调递增区间;
,+∞)为函数g(x)的单调递增区间;当x=
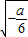 时,g(x)的最小值g(
时,g(x)的最小值g( )=
)=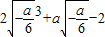 =
=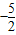 ,
,解得a=-

∴

点评:本题考查的知识点是利用导数研究函数的单调性,函数解析式的求解及常用方法,其中熟练掌握导函数符号与原函数的单调性之间的关系,并又此分析函数的单调区间和极值点是解答的关键.

练习册系列答案
相关题目

 ,求f(x)的解析式.
,求f(x)的解析式.