题目内容
下列几个命题①方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0.
②函数
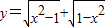 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-3,1].
④设函数y=f(x)定义域为R,则函数y=f(1-x)与y=f(x-1)的图象关于y轴对称.
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1.
其中正确的有 .
【答案】分析:①由方程x2+(a-3)x+a=0的有一个正实根,一个负实根,利用根与系数的关系即可判断出;
②要使函数 有意义,则
有意义,则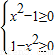 ,解得x即可判断出;
,解得x即可判断出;
③函数f(x)的值域是[-2,2],则函数f(x+1)只是把函数y=f(x)的图象项左平移了一个单位,因此值域没改变;
④举反例:若y=x(x∈R).则f(x-1)=x-1与f(1-x)=1-x关于y轴不对称;
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的有公共点,则|3-x2|=a≥0,可得x2-3=±a,即x2=3±a>0,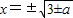 ,即可判断出公共点的个数m.
,即可判断出公共点的个数m.
解答:解:①∵方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则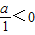 ,即a<0,因此正确;
,即a<0,因此正确;
②要使函数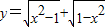 有意义,则
有意义,则 ,解得x=±1,因此y=0(x=±1),故函数既是偶函数,又是奇函数,故不正确;
,解得x=±1,因此y=0(x=±1),故函数既是偶函数,又是奇函数,故不正确;
③函数f(x)的值域是[-2,2],则函数f(x+1)的值域仍然为[-2,2],故不正确;
④举例:若y=x(x∈R).则f(x-1)=x-1与f(1-x)=1-x关于y轴不对称,因此不正确;
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的有公共点,则|3-x2|=a≥0,∴x2-3=±a,即x2=3±a>0,∴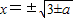 ,
,
因此公共点的个数m可以是2,4,故m的值不可能是1.
综上可知:其中正确的有 ①⑤.
点评:熟练掌握一元二次方程的根与系数的关系、函数的图象与性质等是解题的关键.
②要使函数
 有意义,则
有意义,则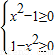 ,解得x即可判断出;
,解得x即可判断出;③函数f(x)的值域是[-2,2],则函数f(x+1)只是把函数y=f(x)的图象项左平移了一个单位,因此值域没改变;
④举反例:若y=x(x∈R).则f(x-1)=x-1与f(1-x)=1-x关于y轴不对称;
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的有公共点,则|3-x2|=a≥0,可得x2-3=±a,即x2=3±a>0,
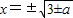 ,即可判断出公共点的个数m.
,即可判断出公共点的个数m.解答:解:①∵方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则
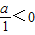 ,即a<0,因此正确;
,即a<0,因此正确;②要使函数
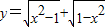 有意义,则
有意义,则 ,解得x=±1,因此y=0(x=±1),故函数既是偶函数,又是奇函数,故不正确;
,解得x=±1,因此y=0(x=±1),故函数既是偶函数,又是奇函数,故不正确;③函数f(x)的值域是[-2,2],则函数f(x+1)的值域仍然为[-2,2],故不正确;
④举例:若y=x(x∈R).则f(x-1)=x-1与f(1-x)=1-x关于y轴不对称,因此不正确;
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的有公共点,则|3-x2|=a≥0,∴x2-3=±a,即x2=3±a>0,∴
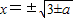 ,
,因此公共点的个数m可以是2,4,故m的值不可能是1.
综上可知:其中正确的有 ①⑤.
点评:熟练掌握一元二次方程的根与系数的关系、函数的图象与性质等是解题的关键.

练习册系列答案
相关题目
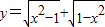 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.