题目内容
下列几个命题
①方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
②A=Q,B=Q,f:x→
,这是一个从集合A到集合B的映射;
③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-3,1];
④函数 f(x)=|x|与函数g(x)=
是同一函数;
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1.
其中正确的有
①方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
②A=Q,B=Q,f:x→
| 1 |
| x |
③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-3,1];
④函数 f(x)=|x|与函数g(x)=
| x2 |
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1.
其中正确的有
①,④,⑤
①,④,⑤
.分析:①根据一元二次方程有异号根的判定方法可知①正确;
②根据映射的定义,举出实例x=0,可判断②错误;
③根据函数图象的平移变换不改变函数的值域,可判断③错误;
④根据两个函数的定义域相等,解析式可化为一致,可判断④正确
⑤画出函数的图象,根据图象可知⑤正确.
②根据映射的定义,举出实例x=0,可判断②错误;
③根据函数图象的平移变换不改变函数的值域,可判断③错误;
④根据两个函数的定义域相等,解析式可化为一致,可判断④正确
⑤画出函数的图象,根据图象可知⑤正确.
解答:解:若方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则
,解得a<0,故①正确;
当x=0时,B中不存在元素与之对应,故f不是一个从集合A到集合B的映射,故②错误;
函数f(x+1)的图象由函数f(x)的图象向左平移一个单位得到,故两个函数的值域相等,故③错误;
函数 f(x)=|x|与函数g(x)=
的定义域均为R,且g(x)=
=|x|,故两个函数为同一函数,故④正确;
曲线y=|3-x2|如图所示:
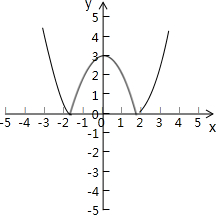
由图可知,m的值可以是0,2,3,4,故⑤正确
故答案为:①,④,⑤
|
当x=0时,B中不存在元素与之对应,故f不是一个从集合A到集合B的映射,故②错误;
函数f(x+1)的图象由函数f(x)的图象向左平移一个单位得到,故两个函数的值域相等,故③错误;
函数 f(x)=|x|与函数g(x)=
| x2 |
| x2 |
曲线y=|3-x2|如图所示:
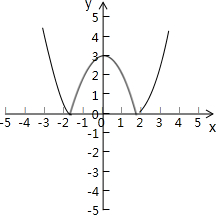
由图可知,m的值可以是0,2,3,4,故⑤正确
故答案为:①,④,⑤
点评:此题是个基础题.考查函数图象的对称变化和一元二次方程根的问题,以及函数奇偶性的判定方法等基础知识,考查学生灵活应用知识分析解决问题的能力.

练习册系列答案
相关题目
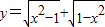 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.