题目内容
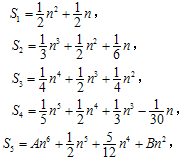 记Sk=1k+2k+3k+…+nk,当k=1,2,3…时,观察如图等式:可以推测,A-B=
记Sk=1k+2k+3k+…+nk,当k=1,2,3…时,观察如图等式:可以推测,A-B=| 1 |
| 4 |
| 1 |
| 4 |
分析:通过观察归纳出:各等式右边各项的系数和为1;最高次项的系数为该项次数的倒数;列出方程求出A,B的值,进一步得到A-B.
解答:解:∵S1=
n2+
n,
S2=
n3+
n2+
n,
S3=
n4+
n3+
n2,
S4=
n5+
n4+
n3-
n
…
归纳分析可得Sk的最高次项为k次项,系数为
等式右边各项的系数和为1;
故A=
,B=-
∴A-B=
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
S3=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
S4=
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 30 |
…
归纳分析可得Sk的最高次项为k次项,系数为
| 1 |
| k |
等式右边各项的系数和为1;
故A=
| 1 |
| 6 |
| 1 |
| 12 |
∴A-B=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查通过观察、归纳猜想结论,并据猜想的结论解决问题,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 n,S2=
n,S2= n,S3=
n,S3= ,S4=
,S4= n,S5=An6+
n,S5=An6+ ,…可以推测,A-B= .
,…可以推测,A-B= .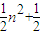 n,S2=
n,S2=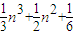 n,S3=
n,S3=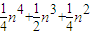 ,S4=
,S4=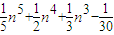 n,S5=An6+
n,S5=An6+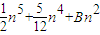 ,…可以推测,A-B= .
,…可以推测,A-B= .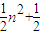 n,S2=
n,S2=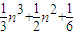 n,S3=
n,S3=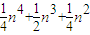 ,S4=
,S4=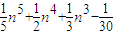 n,S5=An6+
n,S5=An6+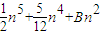 ,…可以推测,A-B= .
,…可以推测,A-B= .