题目内容
P是抛物线y=x2上的点，若过点P的切线方程与直线
垂直，则过P点处的切线方程是 ．
【答案】分析：由过点P的切线方程与直线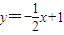
垂直，我们易得切线的斜率，又由切线的斜率等于切点处的导数值，我们不难求出切点坐标，进而得到直线的点斜式方程．
解答：解：∵过点P的切线方程与直线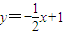
垂直
∴过点P的切线的斜率为2
又∵抛物线方程为y=x2，
则y'=2x，令y'=2x=2，则x=1，
将x=1代入抛物线方程y=x2，得y=1
则P点坐标为（1，1）
则过P点处的切线方程y-1=2（x-1）
即：2x-y-1=0
故答案为：2x-y-1=0
点评：在求直线方程时，应先选择适当的直线方程的形式，并注意各种形式的适用条件，用斜截式及点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线，故在解题时，若采用截距式，应注意分类讨论，判断截距是否为零；若采用点斜式，应先考虑斜率不存在的情况．
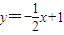垂直，我们易得切线的斜率，又由切线的斜率等于切点处的导数值，我们不难求出切点坐标，进而得到直线的点斜式方程．解答：解：∵过点P的切线方程与直线
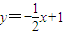垂直∴过点P的切线的斜率为2
又∵抛物线方程为y=x2，
则y'=2x，令y'=2x=2，则x=1，
将x=1代入抛物线方程y=x2，得y=1
则P点坐标为（1，1）
则过P点处的切线方程y-1=2（x-1）
即：2x-y-1=0
故答案为：2x-y-1=0
点评：在求直线方程时，应先选择适当的直线方程的形式，并注意各种形式的适用条件，用斜截式及点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线，故在解题时，若采用截距式，应注意分类讨论，判断截距是否为零；若采用点斜式，应先考虑斜率不存在的情况．
练习册系列答案
相关题目
P是抛物线y=x2上任意一点，则当P点到直线x+y+2=0的距离最小时，P点与该抛物线的准线的距离是（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
如图，设P是抛物线y=x2上一点，且在第一象限．过点P作抛物线的切线，交x轴于Q1点，过Q1点作x轴的垂线，交抛物线于P1点，此时就称P确定了P1．依此类推，可由P1确定P2，…．记Pn（xn，yn），n=0，1，2，…．给出下列三个结论：
