题目内容
给定 A (-2,2),已知 B 是椭圆
+
=1上的动点,F 是左焦点,当|AB|+
|BF|取最小值时,求B的坐标.
| x2 |
| 25 |
| y2 |
| 16 |
| 5 |
| 3 |
分析:由椭圆的第二定义e=
=
可求得BN|=
|BF|,利用化折为直的思想即可求得当|AB|+
|BF|取最小值时,B 的坐标.
| |BF| |
| |BN| |
| 3 |
| 5 |
| 5 |
| 3 |
| 5 |
| 3 |
解答:解:记椭圆的半长轴、半短轴、半焦距分别为a、b、c,离心率为e.则a=5,b=4,c=
=
=3,
e=
=
,左准线为x=-
.
过点B作左准线x=-
的垂线,垂足为N,过A作此准线的垂线,垂足为M.由椭圆定义,
|BN|=
=
|BF|.
于是,|AB|+
|BF|=|AB|+|BN|≥|AN|≥|AM|(定值),等号成立当且仅当B是AM与椭圆的交点时,此时B(-
,2)
所以,当|AB|+
|BF|取最小值时,B的坐标为(-
,2).
| a2-b2 |
| 52-42 |
e=
| c |
| a |
| 3 |
| 5 |
| 25 |
| 3 |
过点B作左准线x=-
| 25 |
| 3 |
|BN|=
| |BF| |
| e |
| 5 |
| 3 |
于是,|AB|+
| 5 |
| 3 |
5
| ||
| 2 |
所以,当|AB|+
| 5 |
| 3 |
5
| ||
| 2 |
点评:本题考查椭圆的简单性质,突出考查椭圆第二定义的应用,考查转化与方程思想,求得BN|=
|BF|是关键,也是难点,属于中档题.
| 5 |
| 3 |

练习册系列答案
相关题目
 上的动点,F 是左焦点,当|AB|+
上的动点,F 是左焦点,当|AB|+ |BF|取最小值时,求B的坐标.
|BF|取最小值时,求B的坐标.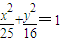 上的动点,F 是左焦点,当|AB|+
上的动点,F 是左焦点,当|AB|+ |BF|取最小值时,求B的坐标.
|BF|取最小值时,求B的坐标.