题目内容
如图,现有一个以∠AOB为圆心角、湖岸OA与OB为半径的扇形湖面AOB.现欲在弧AB上取不同于A,B的点C,用渔网沿着弧AC(弧AC在扇形AOB的弧AB上)、半径OC和线段CD(其中CD∥OA),在该扇形湖面内隔出两个养殖区域--养殖区域Ⅰ和养殖区域Ⅱ.若OA=1cm, ,∠AOC=θ.
,∠AOC=θ.(1)用θ表示CD的长度;
(2)求所需渔网长度(即图中弧AC、半径OC和线段CD长度之和)的取值范围.

【答案】分析:(1)先确定∠COD,再在△OCD中,利用正弦定理,可求CD的长度;
(2)根据所需渔网长度,即图中弧AC、半径OC和线段CD长度之和,确定函数的解析式,利用导数确定函数的最值,即可求得所需渔网长度的取值范围.
解答:解:(1)由CD∥OA,∠AOB= ,∠AOC=θ,得∠OCD=θ,∠ODC=
,∠AOC=θ,得∠OCD=θ,∠ODC= ,∠COD=
,∠COD= -θ.
-θ.
在△OCD中,由正弦定理,得CD= sin(
sin( ),θ∈(0,
),θ∈(0, )(6分)
)(6分)
(2)设渔网的长度为f(θ).
由(1)可知,f(θ)=θ+1+ sin(
sin( ).(8分)
).(8分)
所以f′(θ)=1- cos(
cos( ),因为θ∈(0,
),因为θ∈(0, ),所以
),所以 -θ∈(0,
-θ∈(0,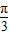 ),
),
令f′(θ)=0,得cos( )=
)=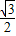 ,所以
,所以 -θ=
-θ= ,所以θ=
,所以θ= .
.
所以f(θ)∈(2, ].
].
故所需渔网长度的取值范围是(2, ].(14分)
].(14分)
点评:本题考查正弦定理的运用,考查函数模型的构建,考查利用导数确定函数的最值,确定函数的解析式是关键.
(2)根据所需渔网长度,即图中弧AC、半径OC和线段CD长度之和,确定函数的解析式,利用导数确定函数的最值,即可求得所需渔网长度的取值范围.
解答:解:(1)由CD∥OA,∠AOB=
 ,∠AOC=θ,得∠OCD=θ,∠ODC=
,∠AOC=θ,得∠OCD=θ,∠ODC= ,∠COD=
,∠COD= -θ.
-θ.在△OCD中,由正弦定理,得CD=
 sin(
sin( ),θ∈(0,
),θ∈(0, )(6分)
)(6分)(2)设渔网的长度为f(θ).
由(1)可知,f(θ)=θ+1+
 sin(
sin( ).(8分)
).(8分)所以f′(θ)=1-
 cos(
cos( ),因为θ∈(0,
),因为θ∈(0, ),所以
),所以 -θ∈(0,
-θ∈(0,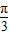 ),
),令f′(θ)=0,得cos(
 )=
)=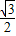 ,所以
,所以 -θ=
-θ= ,所以θ=
,所以θ= .
.| θ | (0, ) ) |  | ( , , ) ) |
| f′(θ) | + | - | |
| f(θ) | 极大值 |
 ].
].故所需渔网长度的取值范围是(2,
 ].(14分)
].(14分)点评:本题考查正弦定理的运用,考查函数模型的构建,考查利用导数确定函数的最值,确定函数的解析式是关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,现有一个以∠AOB为圆心角、湖岸OA与OB为半径的扇形湖面AOB.现欲在弧AB上取不同于A,B的点C,用渔网沿着弧AC(弧AC在扇形AOB的弧AB上)、半径OC和线段CD(其中CD∥OA),在该扇形湖面内隔出两个养殖区域--养殖区域Ⅰ和养殖区域Ⅱ.若OA=1cm,
如图,现有一个以∠AOB为圆心角、湖岸OA与OB为半径的扇形湖面AOB.现欲在弧AB上取不同于A,B的点C,用渔网沿着弧AC(弧AC在扇形AOB的弧AB上)、半径OC和线段CD(其中CD∥OA),在该扇形湖面内隔出两个养殖区域--养殖区域Ⅰ和养殖区域Ⅱ.若OA=1cm, ,∠AOC=θ.
,∠AOC=θ.
 ,∠AOC=θ.
,∠AOC=θ.
 ,∠AOC=θ.
,∠AOC=θ.