题目内容
已知一个圆的圆心为坐标原点,半径为5,从这个圆上任一点p向x轴作垂线PP’,垂足为P’,M为线段PP’上一点,且满足: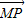 =4
=4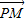
(1)求动点M的轨迹C的方程;
(2)若过电(3,0)且斜率为1的直线交曲线C于A、B两点,求弦AB的长.
【答案】分析:(I)设点M(x,y),点P的坐标为(x,y),由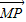 =4
=4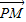 ,可得:x=xo,y=
,可得:x=xo,y= y,P(x,y)在圆x2+y2=25上,所以,x2+y2=25,由此能求出点M的轨迹C的方程.
y,P(x,y)在圆x2+y2=25上,所以,x2+y2=25,由此能求出点M的轨迹C的方程.
(II)设A(x1,y1),B (x2,y2),由已知得直线方程:y=x-3,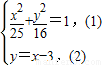 ,整理得41x2-150x-175=0,由韦达定理能导出弦AB的长度.
,整理得41x2-150x-175=0,由韦达定理能导出弦AB的长度.
解答:解:(I)设点M(x,y),点P的坐标为(x,y),由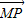 =4
=4 ,
,
可得:x=xo,y= y,
y,
P(x,y)在圆x2+y2=25上,所以,x2+y2=25,
将xo=x,y= ,y代入方程①,得
,y代入方程①,得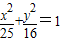 ,
,
故点M的轨迹C的方程为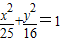 ,
,
(II)设A(x1,y1),B (x2,y2),由已知得直线方程:y=x-3
 ,
,
将(2)代入整理得41x2-150x-175=0
由伟达定理: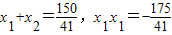 .
.
所以:|AB|=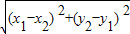 =
= =
=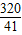 ,
,
故弦AB的长度为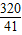 .
.
点评:本题考查点M的轨迹C的方程和求弦AB的长.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
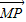 =4
=4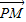 ,可得:x=xo,y=
,可得:x=xo,y= y,P(x,y)在圆x2+y2=25上,所以,x2+y2=25,由此能求出点M的轨迹C的方程.
y,P(x,y)在圆x2+y2=25上,所以,x2+y2=25,由此能求出点M的轨迹C的方程.(II)设A(x1,y1),B (x2,y2),由已知得直线方程:y=x-3,
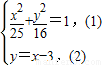 ,整理得41x2-150x-175=0,由韦达定理能导出弦AB的长度.
,整理得41x2-150x-175=0,由韦达定理能导出弦AB的长度.解答:解:(I)设点M(x,y),点P的坐标为(x,y),由
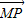 =4
=4 ,
,可得:x=xo,y=
 y,
y,P(x,y)在圆x2+y2=25上,所以,x2+y2=25,
将xo=x,y=
 ,y代入方程①,得
,y代入方程①,得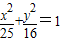 ,
,故点M的轨迹C的方程为
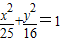 ,
,(II)设A(x1,y1),B (x2,y2),由已知得直线方程:y=x-3
 ,
,将(2)代入整理得41x2-150x-175=0
由伟达定理:
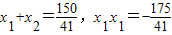 .
.所以:|AB|=
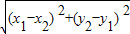 =
= =
=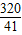 ,
,故弦AB的长度为
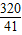 .
.点评:本题考查点M的轨迹C的方程和求弦AB的长.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 ,则线段
,则线段