题目内容
各项都为正数的数列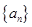 ,其前
,其前 项的和为
项的和为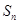 ,且
,且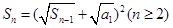 ,若
,若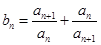 ,且数列
,且数列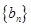 的前
的前 项的和为
项的和为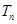 ,则
,则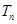 = .
= .
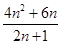
解析试题分析:本题涉及涉及到数列的前 和
和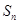 的关系,一般要用到关系式
的关系,一般要用到关系式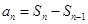 ,由
,由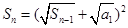 得
得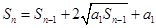 ,所以
,所以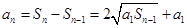 ,于是
,于是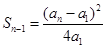 ,
,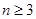 时,
时,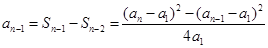 ,化简得:
,化简得: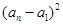
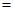
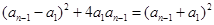 ,即
,即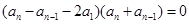 ,由于数列
,由于数列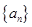 各项为正,故
各项为正,故 ,又
,又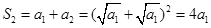 ,即
,即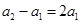 ,因此数列
,因此数列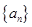 是等差数列,公比为
是等差数列,公比为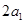 ,所以
,所以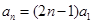 .
.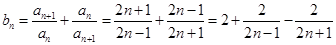 ,
,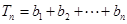
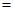

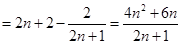 .
.
考点: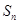 与
与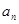 的关系,裂项相消求和.
的关系,裂项相消求和.

练习册系列答案
相关题目
设等比数列 的公比为
的公比为 ,前n项和为
,前n项和为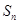 ,若
,若 ,
,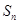 ,
,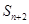 成等差数列,则公比
成等差数列,则公比 为( ).
为( ).
A.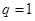 | B. | C. 或 或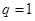 | D. 或 或 |
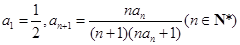 ,则数列{an}的前2012项的和为 .
,则数列{an}的前2012项的和为 .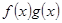 =ax,且f′(x)g(x)+f(x)·g′(x)<0,
=ax,且f′(x)g(x)+f(x)·g′(x)<0,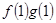 +
+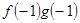 =
=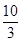 ,若有穷数列{
,若有穷数列{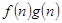 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于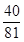 ,则n等于 .
,则n等于 .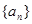 是等和数列,且
是等和数列,且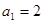 ,公和为5,那么这个数列的前21项和
,公和为5,那么这个数列的前21项和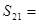 .
.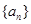 的前
的前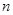 项的和为
项的和为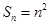 ,则
,则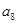 =_________.
=_________.
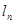 :
: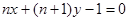 (
(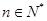 )与坐标轴所围成的直角三角形的面积为
)与坐标轴所围成的直角三角形的面积为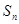 ,则
,则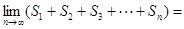 .
.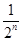 ,n∈N?,则a3=________.
,n∈N?,则a3=________.