题目内容
(2013•泰安一模)某产品按行业生产标准分成6个等级,等级系数ξ依次为1,2,3,4,5,6,按行业规定产品的等级系数ξ≥5的为一等品,3≤ξ<5的为二等品,ξ<3的为三等品.
若某工厂生产的产品均符合行业标准,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下;

(I)以此30件产品的样本来估计该厂产品的总体情况,试分别求出该厂生产原一等品、二等品和三等品的概率;
(II)已知该厂生产一件产品的利润y(单位:元)与产品的等级系数ζ的关系式为y=
,若从该厂大量产品中任取两件,其利润记为Z,求Z的分布列和数学期望.
若某工厂生产的产品均符合行业标准,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下;

(I)以此30件产品的样本来估计该厂产品的总体情况,试分别求出该厂生产原一等品、二等品和三等品的概率;
(II)已知该厂生产一件产品的利润y(单位:元)与产品的等级系数ζ的关系式为y=
|
分析:(I)由样本数据,结合行业规定,确定一等品有6件,二等品有9件,三等品有15件,即可估计该厂生产的产品的一等品率、二等品率和三等品率;
(II)确定Z的可能取值为:2,3,4,5,6,8.用样本的频率分布估计总体分布,将频率视为概率,可得Z的分布列,从而可求数学期望.
(II)确定Z的可能取值为:2,3,4,5,6,8.用样本的频率分布估计总体分布,将频率视为概率,可得Z的分布列,从而可求数学期望.
解答:解:(I)由样本数据知,30件产品中等级系数ξ≥7有6件,即一等品有6件,二等品有9件,三等品有15件-----------------------------------------------------------(3分)
∴样本中一等品的频率为
=0.2,故估计该厂生产的产品的一等品率为0.2--------(4分)
二等品的频率为
=0.3,故估计该厂生产的产品的二等品率为0.3;--------------(5分)
三等品的频率为
=0.5,故估计该厂生产的产品的三等品的频率为0.5.----------(6分)
(II)∵Z的可能取值为:2,3,4,5,6,8.
用样本的频率分布估计总体分布,将频率视为概率,可得
P(Z=2)=0.5×0.5=
,P(Z=3)=2×
×
=
,
P(Z=4)=
×
=
,P(Z=5)=2×
×
=
,
P(Z=6)=2×
×
=
,P(Z=8)=
×
=
,
∴可得X的分布列如下:----------------------------------------------------(10分)
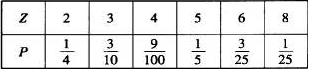
其数学期望EX=3.8(元)-----------------------------(12分)
∴样本中一等品的频率为
| 6 |
| 30 |
二等品的频率为
| 9 |
| 30 |
三等品的频率为
| 15 |
| 30 |
(II)∵Z的可能取值为:2,3,4,5,6,8.
用样本的频率分布估计总体分布,将频率视为概率,可得
P(Z=2)=0.5×0.5=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 10 |
| 3 |
| 10 |
P(Z=4)=
| 3 |
| 10 |
| 3 |
| 10 |
| 9 |
| 100 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
P(Z=6)=2×
| 3 |
| 10 |
| 1 |
| 5 |
| 3 |
| 25 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 25 |
∴可得X的分布列如下:----------------------------------------------------(10分)

其数学期望EX=3.8(元)-----------------------------(12分)
点评:本题考查统计知识,考查离散型随机变量的分布列与期望,解题时利用样本的频率分布估计总体分布,将频率视为概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目