题目内容
已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且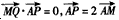 。
。
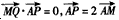 。
。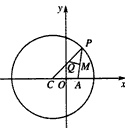
(1)当点P在圆上运动时,求点Q的轨迹方程;
(2)设过点(0,2)且斜率为2的直线l与(1)中所求的曲线交于B,D两点,O为坐标原点,求△BDO的面积。
(2)设过点(0,2)且斜率为2的直线l与(1)中所求的曲线交于B,D两点,O为坐标原点,求△BDO的面积。
解:(1)由题意,MQ是线段AP的垂直平分线,
故|QC|+|QA|=|QC|+|QP|=|CP|
 >|CA|=2
>|CA|=2
于是点Q的轨迹是以点C,A为焦点,半焦距c=1,长半轴 的椭圆,短半轴
的椭圆,短半轴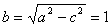
∴点O的轨迹方程是: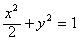 。
。
(2)因直线l过点(0,2)且斜率为2,则直线l的方程为:y=2x+2,即2x-y+2=0,
故点O(0,0)到直线l的距离d=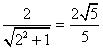
把y=2x+2代入(1)中的方程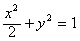 化简,
化简,
得9x2+16x+6=0
∴Δ=162-4×9×6=40>0
设B(x1,y1),D(x2,y2),
则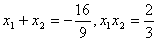
∴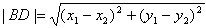
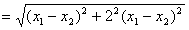
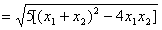
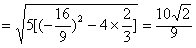
∴△BDO的面积为
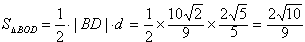 。
。
故|QC|+|QA|=|QC|+|QP|=|CP|
 >|CA|=2
>|CA|=2于是点Q的轨迹是以点C,A为焦点,半焦距c=1,长半轴
 的椭圆,短半轴
的椭圆,短半轴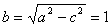
∴点O的轨迹方程是:
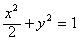 。
。(2)因直线l过点(0,2)且斜率为2,则直线l的方程为:y=2x+2,即2x-y+2=0,
故点O(0,0)到直线l的距离d=
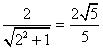
把y=2x+2代入(1)中的方程
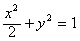 化简,
化简,得9x2+16x+6=0
∴Δ=162-4×9×6=40>0
设B(x1,y1),D(x2,y2),
则
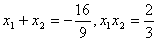
∴
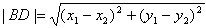
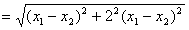
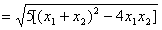
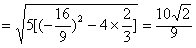
∴△BDO的面积为
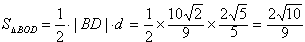 。
。
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
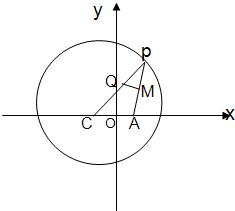 已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且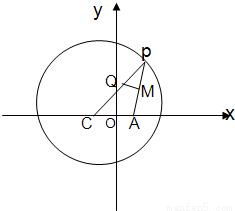 已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且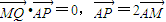 .
.