题目内容
甲、乙两位篮球运动员进行定点投篮,甲投篮一次命中的概率为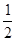 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为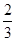 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响.
(1)求甲至多命中1个球且乙至少命中1个球的概率;
(2)若规定每投篮一次命中得3分,未命中得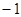 分,求乙所得分数
分,求乙所得分数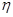 的概率分布和数学期望.
的概率分布和数学期望.
【答案】
(1)80:81
(2) 分布列如下:
分布列如下:
|
|
|
0 |
4 |
8 |
12 |
|
P |
|
|
|
|
|
13分

【解析】
试题分析:解:(1)设“甲至多命中1个球””为事件A,“乙至少命中1个球”为事件B, 1分
由题意得,
 5分
5分
∴甲至多命中2个球且乙至少命中2个球的概率为
 6分
6分
(2)乙所得分数 的可能取值为
的可能取值为 , 7分
, 7分
则 ,
, ,
,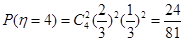 ,
,
 ,
, 11分
11分
 分布列如下:
分布列如下:
|
|
|
0 |
4 |
8 |
12 |
|
P |
|
|
|
|
|
13分
 14分
14分
考点:分布列的性质以及概率的求解
点评:主要是考查了分布列的求解以及独立事件的概率,属于中档题。

练习册系列答案
相关题目


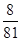



 ,乙投篮命中的概率为
,乙投篮命中的概率为 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.