题目内容
已知函数f(x)的导数f′(x)=3x2-3ax,f(![]() 0)=b,a,b为实数,1<a<2.
0)=b,a,b为实数,1<a<2.
(1)若f(x)在区间[-1,1]上的最小值、最大值分别为-2、1,求a、b的值;
(2)在(1)的条件下,求经过点P(2,1)且与曲线f(x)相切的直线l的方程;
(3)设函数F(x)=[f′(x)+6x+1]·e2x,试判断函数F(x)的极值点个数.
(1)由已知得,f(x)=x3-![]() ax2+b,由f′(x)=0,得x1=0,x2=a.
ax2+b,由f′(x)=0,得x1=0,x2=a.
∵x∈[-1,1],1<a<2,∴当x∈[-1,0)时,f′(x)>0,f(x)递增;当x∈(0,1]时,f′(x)<0,f(x)递减,∴f(x)在区间[-1,1]上的最大值为f(0)=b,
∴b=1.
又f(1)=1-![]() a+1=2-
a+1=2-![]() a,f(-1)=-1-
a,f(-1)=-1-![]() a+1=-
a+1=-![]() a,∴f(-1)<f(1).
a,∴f(-1)<f(1).
由题意得f(-1)=-2,即-![]() a=-2,得a=
a=-2,得a=![]() ,故a=
,故a=![]() ,b=1为所求.
,b=1为所求.
(2)由(1)得f(x)=x3-2x2+1,f′(x)=3x2-4x,点P(2,1)在曲线f(x)上.
①当切点为P(2,1)时,切线l的斜率k=f′(x)|x=2=4,
∴l的方程为y-1=![]() 4(x-2),即4x-y-7=0.
4(x-2),即4x-y-7=0.
②当点P不是切点时,设切点O(x0,y0)(x0≠2),切线l的斜率
k=f′(x)|x=x0=3x![]() -4x0,
-4x0,
∴l的方程为y-y0=(3x![]() -4x0)(x-x0),
-4x0)(x-x0),
又点P(2,1)在l上,∴1-y0=(3x![]() -4x0)(2-x0),
-4x0)(2-x0),
∴1-(x![]() -2x
-2x![]() +1)=(3x
+1)=(3x![]() -4x0)(2-x0),
-4x0)(2-x0),
∴x![]() (2-x0)=(3x
(2-x0)=(3x![]() -4x0)(2-x0),
-4x0)(2-x0),
∴x![]() =3x
=3x![]() -4x0,即2x0(x0-2)=0,
-4x0,即2x0(x0-2)=0,
∴x0=0,∴切线l的方程为y=1.
故所求切线l的方程为4x-y-7=0或y=1.
(3)F(x)=(3x2-3ax+6x+1)·e2x=[3x2![]() -3(a-2)x+1]·e2x,
-3(a-2)x+1]·e2x,
∴F′![]() (x)=[6x-3(a-2)]·e2x+2[3x2-3(a-2)x+1]·e2x=[6x2-6(a-3)x+8-3a]·e2x.
(x)=[6x-3(a-2)]·e2x+2[3x2-3(a-2)x+1]·e2x=[6x2-6(a-3)x+8-3a]·e2x.
二次函数y=6x2-6(a-3)x+8-3a的判别式为
Δ=36(a-3)2-24(8-3a)=12(3a2-12a+11)=12[3·(a-2)2-1],令Δ≤0,得:(a-2)2≤![]() ,2-
,2-![]() ≤a≤2+
≤a≤2+![]() ,令Δ>0时,得a<2-
,令Δ>0时,得a<2-![]() 或a>2+
或a>2+![]() .
.
∵e2x>0,1<a<2,∴当2-![]() ≤a<2时,F′(x)≥0,函数F(x)为单调递增函数,极值点个数为0;
≤a<2时,F′(x)≥0,函数F(x)为单调递增函数,极值点个数为0;
当1<a<2-![]() 时,此时方程F′(x)=0有两个不相等的实数根,根据极值点的定义,可知函数F(x)有两个极值点.
时,此时方程F′(x)=0有两个不相等的实数根,根据极值点的定义,可知函数F(x)有两个极值点.

 的图象如图所示,那么函数f (x)的图象最有可能的是( )
的图象如图所示,那么函数f (x)的图象最有可能的是( )
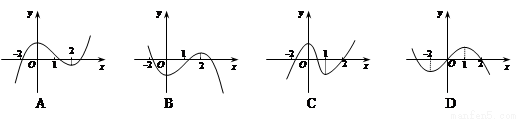
 ,且满足f(x)=2x
,且满足f(x)=2x +ln x,则
+ln x,则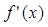 的图像如左图所示,那么函数f(x)的图像最有可能的
的图像如左图所示,那么函数f(x)的图像最有可能的