题目内容
试比较下列各式的大小(不写过程)
(1)
-1与
-
;
(2)
-
与
-
通过上式请你推测出
-
与
-
,n≥2,n∈N*的大小,并加以证明.
(1)
| 2 |
| 3 |
| 2 |
(2)
| 3 |
| 2 |
| 4 |
| 3 |
通过上式请你推测出
| n |
| n-1 |
| n+1 |
| n |
分析:把给出的两组数作查后再求平方差的符号,得到;两组数的大小关系,从而推测出
-
与
-
,n≥2,n∈N*的大小,运用同样的方法加以证明.
| n |
| n-1 |
| n+1 |
| n |
解答:解:(1)因为(
-1)-(
-
)=2
-(
+1),而(2
)2-(
+1)2=4-2
=
-
>0,
所以
-1>
-
;
(2)因为(
-
)-(
-
)=2
-(
+
),而(2
)2-(
+
)2=
-
>0,
所以
-
>
-
;
由上推测
-
>
-
,n≥2,n∈N*.
事实上,(
-
)-(
-
)=2
-(
+
),
因为(2
)2-(
+
)2=2n-2
=(
-
)2>0.
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 16 |
| 12 |
所以
| 2 |
| 3 |
| 2 |
(2)因为(
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 4 |
| 2 |
| 36 |
| 32 |
所以
| 3 |
| 2 |
| 4 |
| 3 |
由上推测
| n |
| n-1 |
| n+1 |
| n |
事实上,(
| n |
| n-1 |
| n+1 |
| n |
| n |
| n-1 |
| n+1 |
因为(2
| n |
| n-1 |
| n+1 |
| n-1 |
| n+1 |
| n-1 |
| n+1 |
点评:本题考查了不等式的大小比较,考查了归纳推理,训练了平方差法比较两个正数的大小,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 与
与

 -
- 与
与 (n
(n 2,n
2,n N)的大小,并用分析法证明
N)的大小,并用分析法证明 与
与

 与
与 且n
且n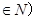 的大小,并用分析法加以证明。
的大小,并用分析法加以证明。 ;
; 与
与
 与
与 ,n≥2,n∈N*的大小,并加以证明.
,n≥2,n∈N*的大小,并加以证明.